探索性分析
首先读入数据housing。将数据导入到data变量中,观察data变量的结构。
str(data)## 'data.frame': 2919 obs. of 81 variables:
## $ Id : int 1 2 3 4 5 6 7 8 9 10 ...
## $ MSSubClass : int 60 20 60 70 60 50 20 60 50 190 ...
## $ MSZoning : Factor w/ 5 levels "C (all)","FV",..: 4 4 4 4 4 4 4 4 5 4 ...
## $ LotFrontage : int 65 80 68 60 84 85 75 NA 51 50 ...
## $ LotArea : int 8450 9600 11250 9550 14260 14115 10084 10382 6120 7420 ...
## $ Street : Factor w/ 2 levels "Grvl","Pave": 2 2 2 2 2 2 2 2 2 2 ...
## $ Alley : Factor w/ 2 levels "Grvl","Pave": NA NA NA NA NA NA NA NA NA NA ...
## $ LotShape : Factor w/ 4 levels "IR1","IR2","IR3",..: 4 4 1 1 1 1 4 1 4 4 ...
## $ LandContour : Factor w/ 4 levels "Bnk","HLS","Low",..: 4 4 4 4 4 4 4 4 4 4 ...
## $ Utilities : Factor w/ 2 levels "AllPub","NoSeWa": 1 1 1 1 1 1 1 1 1 1 ...
## $ LotConfig : Factor w/ 5 levels "Corner","CulDSac",..: 5 3 5 1 3 5 5 1 5 1 ...
## $ LandSlope : Factor w/ 3 levels "Gtl","Mod","Sev": 1 1 1 1 1 1 1 1 1 1 ...
## $ Neighborhood : Factor w/ 25 levels "Blmngtn","Blueste",..: 6 25 6 7 14 12 21 17 18 4 ...
## $ Condition1 : Factor w/ 9 levels "Artery","Feedr",..: 3 2 3 3 3 3 3 5 1 1 ...
## $ Condition2 : Factor w/ 8 levels "Artery","Feedr",..: 3 3 3 3 3 3 3 3 3 1 ...
## $ BldgType : Factor w/ 5 levels "1Fam","2fmCon",..: 1 1 1 1 1 1 1 1 1 2 ...
## $ HouseStyle : Factor w/ 8 levels "1.5Fin","1.5Unf",..: 6 3 6 6 6 1 3 6 1 2 ...
## $ OverallQual : int 7 6 7 7 8 5 8 7 7 5 ...
## $ OverallCond : int 5 8 5 5 5 5 5 6 5 6 ...
## $ YearBuilt : int 2003 1976 2001 1915 2000 1993 2004 1973 1931 1939 ...
## $ YearRemodAdd : int 2003 1976 2002 1970 2000 1995 2005 1973 1950 1950 ...
## $ RoofStyle : Factor w/ 6 levels "Flat","Gable",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ RoofMatl : Factor w/ 8 levels "ClyTile","CompShg",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ Exterior1st : Factor w/ 15 levels "AsbShng","AsphShn",..: 13 9 13 14 13 13 13 7 4 9 ...
## $ Exterior2nd : Factor w/ 16 levels "AsbShng","AsphShn",..: 14 9 14 16 14 14 14 7 16 9 ...
## $ MasVnrType : Factor w/ 4 levels "BrkCmn","BrkFace",..: 2 3 2 3 2 3 4 4 3 3 ...
## $ MasVnrArea : int 196 0 162 0 350 0 186 240 0 0 ...
## $ ExterQual : Factor w/ 4 levels "Ex","Fa","Gd",..: 3 4 3 4 3 4 3 4 4 4 ...
## $ ExterCond : Factor w/ 5 levels "Ex","Fa","Gd",..: 5 5 5 5 5 5 5 5 5 5 ...
## $ Foundation : Factor w/ 6 levels "BrkTil","CBlock",..: 3 2 3 1 3 6 3 2 1 1 ...
## $ BsmtQual : Factor w/ 4 levels "Ex","Fa","Gd",..: 3 3 3 4 3 3 1 3 4 4 ...
## $ BsmtCond : Factor w/ 4 levels "Fa","Gd","Po",..: 4 4 4 2 4 4 4 4 4 4 ...
## $ BsmtExposure : Factor w/ 4 levels "Av","Gd","Mn",..: 4 2 3 4 1 4 1 3 4 4 ...
## $ BsmtFinType1 : Factor w/ 6 levels "ALQ","BLQ","GLQ",..: 3 1 3 1 3 3 3 1 6 3 ...
## $ BsmtFinSF1 : int 706 978 486 216 655 732 1369 859 0 851 ...
## $ BsmtFinType2 : Factor w/ 6 levels "ALQ","BLQ","GLQ",..: 6 6 6 6 6 6 6 2 6 6 ...
## $ BsmtFinSF2 : int 0 0 0 0 0 0 0 32 0 0 ...
## $ BsmtUnfSF : int 150 284 434 540 490 64 317 216 952 140 ...
## $ TotalBsmtSF : int 856 1262 920 756 1145 796 1686 1107 952 991 ...
## $ Heating : Factor w/ 6 levels "Floor","GasA",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ HeatingQC : Factor w/ 5 levels "Ex","Fa","Gd",..: 1 1 1 3 1 1 1 1 3 1 ...
## $ CentralAir : Factor w/ 2 levels "N","Y": 2 2 2 2 2 2 2 2 2 2 ...
## $ Electrical : Factor w/ 5 levels "FuseA","FuseF",..: 5 5 5 5 5 5 5 5 2 5 ...
## $ X1stFlrSF : int 856 1262 920 961 1145 796 1694 1107 1022 1077 ...
## $ X2ndFlrSF : int 854 0 866 756 1053 566 0 983 752 0 ...
## $ LowQualFinSF : int 0 0 0 0 0 0 0 0 0 0 ...
## $ GrLivArea : int 1710 1262 1786 1717 2198 1362 1694 2090 1774 1077 ...
## $ BsmtFullBath : int 1 0 1 1 1 1 1 1 0 1 ...
## $ BsmtHalfBath : int 0 1 0 0 0 0 0 0 0 0 ...
## $ FullBath : int 2 2 2 1 2 1 2 2 2 1 ...
## $ HalfBath : int 1 0 1 0 1 1 0 1 0 0 ...
## $ BedroomAbvGr : int 3 3 3 3 4 1 3 3 2 2 ...
## $ KitchenAbvGr : int 1 1 1 1 1 1 1 1 2 2 ...
## $ KitchenQual : Factor w/ 4 levels "Ex","Fa","Gd",..: 3 4 3 3 3 4 3 4 4 4 ...
## $ TotRmsAbvGrd : int 8 6 6 7 9 5 7 7 8 5 ...
## $ Functional : Factor w/ 7 levels "Maj1","Maj2",..: 7 7 7 7 7 7 7 7 3 7 ...
## $ Fireplaces : int 0 1 1 1 1 0 1 2 2 2 ...
## $ FireplaceQu : Factor w/ 5 levels "Ex","Fa","Gd",..: NA 5 5 3 5 NA 3 5 5 5 ...
## $ GarageType : Factor w/ 6 levels "2Types","Attchd",..: 2 2 2 6 2 2 2 2 6 2 ...
## $ GarageYrBlt : int 2003 1976 2001 1998 2000 1993 2004 1973 1931 1939 ...
## $ GarageFinish : Factor w/ 3 levels "Fin","RFn","Unf": 2 2 2 3 2 3 2 2 3 2 ...
## $ GarageCars : int 2 2 2 3 3 2 2 2 2 1 ...
## $ GarageArea : int 548 460 608 642 836 480 636 484 468 205 ...
## $ GarageQual : Factor w/ 5 levels "Ex","Fa","Gd",..: 5 5 5 5 5 5 5 5 2 3 ...
## $ GarageCond : Factor w/ 5 levels "Ex","Fa","Gd",..: 5 5 5 5 5 5 5 5 5 5 ...
## $ PavedDrive : Factor w/ 3 levels "N","P","Y": 3 3 3 3 3 3 3 3 3 3 ...
## $ WoodDeckSF : int 0 298 0 0 192 40 255 235 90 0 ...
## $ OpenPorchSF : int 61 0 42 35 84 30 57 204 0 4 ...
## $ EnclosedPorch: int 0 0 0 272 0 0 0 228 205 0 ...
## $ X3SsnPorch : int 0 0 0 0 0 320 0 0 0 0 ...
## $ ScreenPorch : int 0 0 0 0 0 0 0 0 0 0 ...
## $ PoolArea : int 0 0 0 0 0 0 0 0 0 0 ...
## $ PoolQC : Factor w/ 3 levels "Ex","Fa","Gd": NA NA NA NA NA NA NA NA NA NA ...
## $ Fence : Factor w/ 4 levels "GdPrv","GdWo",..: NA NA NA NA NA 3 NA NA NA NA ...
## $ MiscFeature : Factor w/ 4 levels "Gar2","Othr",..: NA NA NA NA NA 3 NA 3 NA NA ...
## $ MiscVal : int 0 0 0 0 0 700 0 350 0 0 ...
## $ MoSold : int 2 5 9 2 12 10 8 11 4 1 ...
## $ YrSold : int 2008 2007 2008 2006 2008 2009 2007 2009 2008 2008 ...
## $ SaleType : Factor w/ 9 levels "COD","Con","ConLD",..: 9 9 9 9 9 9 9 9 9 9 ...
## $ SaleCondition: Factor w/ 6 levels "Abnorml","AdjLand",..: 5 5 5 1 5 5 5 5 1 5 ...
## $ SalePrice : int 208500 181500 223500 140000 250000 143000 307000 200000 129900 118000 ...从上面可以观察到,变量主要分为数值型变量和因子型变量。
bianliang <- sapply(data,class)
table(bianliang)## bianliang
## factor integer
## 43 38#对每列就是变量使用class函数然后使用table函数输出类型数据中有43个因子型变量和38个整数型变量。
变量处理
通过对数据观察发现,存在许多缺失值,首先处理数据的缺失值。
queshizhi<-sapply(data,function(x) sum(is.na(x)))
#使用r语言中的function函数计算为na的个数
# 按照缺失的大小进行排名
queshi <-sort(queshizhi,decreasing = T)
queshi[queshi>0]## PoolQC MiscFeature Alley Fence SalePrice FireplaceQu
## 2909 2814 2721 2348 1459 1420
## LotFrontage GarageYrBlt GarageFinish GarageQual GarageCond GarageType
## 486 159 159 159 159 157
## BsmtCond BsmtExposure BsmtQual BsmtFinType2 BsmtFinType1 MasVnrType
## 82 82 81 80 79 24
## MasVnrArea MSZoning Utilities BsmtFullBath BsmtHalfBath Functional
## 23 4 2 2 2 2
## Exterior1st Exterior2nd BsmtFinSF1 BsmtFinSF2 BsmtUnfSF TotalBsmtSF
## 1 1 1 1 1 1
## Electrical KitchenQual GarageCars GarageArea SaleType
## 1 1 1 1 1我们进一步看这些缺失的变量的情况。
summary(data[,names(queshi)[queshi>0]])## PoolQC MiscFeature Alley Fence SalePrice FireplaceQu
## Ex : 4 Gar2: 5 Grvl: 120 GdPrv: 118 Min. : 34900 Ex : 43
## Fa : 2 Othr: 4 Pave: 78 GdWo : 112 1st Qu.:129975 Fa : 74
## Gd : 4 Shed: 95 NA's:2721 MnPrv: 329 Median :163000 Gd : 744
## NA's:2909 TenC: 1 MnWw : 12 Mean :180921 Po : 46
## NA's:2814 NA's :2348 3rd Qu.:214000 TA : 592
## Max. :755000 NA's:1420
## NA's :1459
## LotFrontage GarageYrBlt GarageFinish GarageQual GarageCond
## Min. : 21.00 Min. :1895 Fin : 719 Ex : 3 Ex : 3
## 1st Qu.: 59.00 1st Qu.:1960 RFn : 811 Fa : 124 Fa : 74
## Median : 68.00 Median :1979 Unf :1230 Gd : 24 Gd : 15
## Mean : 69.31 Mean :1978 NA's: 159 Po : 5 Po : 14
## 3rd Qu.: 80.00 3rd Qu.:2002 TA :2604 TA :2654
## Max. :313.00 Max. :2207 NA's: 159 NA's: 159
## NA's :486 NA's :159
## GarageType BsmtCond BsmtExposure BsmtQual BsmtFinType2 BsmtFinType1
## 2Types : 23 Fa : 104 Av : 418 Ex : 258 ALQ : 52 ALQ :429
## Attchd :1723 Gd : 122 Gd : 276 Fa : 88 BLQ : 68 BLQ :269
## Basment: 36 Po : 5 Mn : 239 Gd :1209 GLQ : 34 GLQ :849
## BuiltIn: 186 TA :2606 No :1904 TA :1283 LwQ : 87 LwQ :154
## CarPort: 15 NA's: 82 NA's: 82 NA's: 81 Rec : 105 Rec :288
## Detchd : 779 Unf :2493 Unf :851
## NA's : 157 NA's: 80 NA's: 79
## MasVnrType MasVnrArea MSZoning Utilities BsmtFullBath
## BrkCmn : 25 Min. : 0.0 C (all): 25 AllPub:2916 Min. :0.0000
## BrkFace: 879 1st Qu.: 0.0 FV : 139 NoSeWa: 1 1st Qu.:0.0000
## None :1742 Median : 0.0 RH : 26 NA's : 2 Median :0.0000
## Stone : 249 Mean : 102.2 RL :2265 Mean :0.4299
## NA's : 24 3rd Qu.: 164.0 RM : 460 3rd Qu.:1.0000
## Max. :1600.0 NA's : 4 Max. :3.0000
## NA's :23 NA's :2
## BsmtHalfBath Functional Exterior1st Exterior2nd
## Min. :0.00000 Typ :2717 VinylSd:1025 VinylSd:1014
## 1st Qu.:0.00000 Min2 : 70 MetalSd: 450 MetalSd: 447
## Median :0.00000 Min1 : 65 HdBoard: 442 HdBoard: 406
## Mean :0.06136 Mod : 35 Wd Sdng: 411 Wd Sdng: 391
## 3rd Qu.:0.00000 Maj1 : 19 Plywood: 221 Plywood: 270
## Max. :2.00000 (Other): 11 (Other): 369 (Other): 390
## NA's :2 NA's : 2 NA's : 1 NA's : 1
## BsmtFinSF1 BsmtFinSF2 BsmtUnfSF TotalBsmtSF
## Min. : 0.0 Min. : 0.00 Min. : 0.0 Min. : 0.0
## 1st Qu.: 0.0 1st Qu.: 0.00 1st Qu.: 220.0 1st Qu.: 793.0
## Median : 368.5 Median : 0.00 Median : 467.0 Median : 989.5
## Mean : 441.4 Mean : 49.58 Mean : 560.8 Mean :1051.8
## 3rd Qu.: 733.0 3rd Qu.: 0.00 3rd Qu.: 805.5 3rd Qu.:1302.0
## Max. :5644.0 Max. :1526.00 Max. :2336.0 Max. :6110.0
## NA's :1 NA's :1 NA's :1 NA's :1
## Electrical KitchenQual GarageCars GarageArea SaleType
## FuseA: 188 Ex : 205 Min. :0.000 Min. : 0.0 WD :2525
## FuseF: 50 Fa : 70 1st Qu.:1.000 1st Qu.: 320.0 New : 239
## FuseP: 8 Gd :1151 Median :2.000 Median : 480.0 COD : 87
## Mix : 1 TA :1492 Mean :1.767 Mean : 472.9 ConLD : 26
## SBrkr:2671 NA's: 1 3rd Qu.:2.000 3rd Qu.: 576.0 CWD : 12
## NA's : 1 Max. :5.000 Max. :1488.0 (Other): 29
## NA's :1 NA's :1 NA's : 1对于缺失数据很多的PoolQC、MiscFeature、Alley、Fence、FireplaceQu这些变量,无法进行插值补充,我们直接去除这些变量。
# 去除如下变量
quchu <- names(data) %in% c("PoolQC","MiscFeature","Alley","Fence","FireplaceQu")
data <- data[!quchu]
#使用逻辑运算符提取出变量然后去除相对应的列去除了NA值较多的变量之后,对Garage系列的变量和Bsmt系列的变量通过网上搜索发现这是车库和地下室的相关数据,对这些NA值我们使用NONE来替代缺失值。
通过查询描述文件得知,GarrageYrBLt为车库建造年份,使用房子的建造年份代替。
data$GarageYrBlt[is.na(data$GarageYrBlt)] <- data$YearBuilt[is.na(data$GarageYrBlt)]补全缺失值
对LotFrontage是房屋到街道的距离,用中位数来填充缺失。
data$LotFrontage[is.na(data$LotFrontage)] <- median(data$LotFrontage, na.rm = T)
#使用中位数补全MasVnrType是外墙的装饰材料,对售价的影响不大。用NONE补充
data[["MasVnrType"]][is.na(data[["MasVnrType"]])] = "None"MasVnrArea是外墙装饰材料的面积,用数值0来填充。
data[["MasVnrArea"]][is.na(data[["MasVnrArea"]])] <- 0Utilities 没有分析的意义,直接去除
data$Utilities <- NULL变量 BsmtFullBath BsmtHalfBath BsmtFinSF1 BsmtFinSF2 BsmtUnfSF TotalBsmtSF GarageCars GarageArea 是和车库和地下室相关的变量,是数值型变量,补充为0就可以。
drop <- c("BsmtFullBath","BsmtHalfBath","BsmtFinSF1","BsmtFinSF2","BsmtUnfSF","TotalBsmtSF","GarageCars","GarageArea")
for (x in drop ) data[[x]][is.na(data[[x]])] <- 0
#使用简单的循环进行数据清洗MSZoning,Functional,Exterior1st,Exterior2nd,KitchenQual,Electrical,SaleType,这些是因子型变量,并且缺失值很少,用最高频率的因子来替代即可。
tidai <- c("MSZoning","Functional","Exterior1st","Exterior2nd","KitchenQual","Electrical","SaleType")
for (x in tidai ) data[[x]][is.na(data[[x]])] <- levels(data[[x]])[which.max(table(data[[x]]))]# 通过SalePrice是否为空来区分训练集和测试集
train <- data[!is.na(data$SalePrice), ]
test <- data[is.na(data$SalePrice), ]建立模型
数据中自变量很多,根据常识我们要从自变量中选出对房价影响最大的因素。我们可以首先人工筛选出一些对房价影响大的因素,然后再添加新的变量来看是否对模型会有改善。 在国内的话,房价的主要影响因素有房子面积、房子所在的区域、小区等,房龄、房型(小高层、多层、别墅等)、特殊场景(地铁房、学区房等)、装修等也会影响价格。对美国房价来说其实也差不多。因此我们选择如下的变量作为观测。
- LotArea 房子的面积
- Neighborhood 城市街区 用来初步代替 区域、小区
- Condition1 Condition2 附近的交通情况
- BldgType 房屋类型 独栋别墅、联排别墅
- HouseStyle 房子的层数
- YearBuilt 房子建造的年份
- YearRemodAdd: 房子的改造年份
- OverallQual: 房子整体质量,考量材料和完成度
- OverallCond:房子整体条件
观察变量关系
写出函数来观察因子型变量和数值型变量的分布图。
# 加载库
library(ggplot2)
library(Rmisc)## 载入需要的程辑包:lattice## 载入需要的程辑包:plyr# 将对于因子变量画图
plot2_factor <- function(var_name){
plots <- list()
plots[[1]] <- ggplot(train, aes_string(x = var_name, fill = var_name) ) +
geom_bar() +
guides(fill = FALSE) +
ggtitle(paste("count of ", var_name)) +
theme(axis.text.x = element_text(angle = 90, hjust =1))
plots[[2]] <- ggplot(train, aes_string(x = var_name, y = "SalePrice", fill = var_name) ) +
geom_boxplot() +
guides(fill = FALSE) +
ggtitle(paste( var_name, " vs SalePrice")) +
theme(axis.text.x = element_text(angle = 90, hjust =1))
multiplot(plotlist = plots, cols = 2)
}
# 对于连续数字变量画图
plot2_number <- function(var_name){
plots <- list()
plots[[1]] <- ggplot(train, aes_string(x = var_name) ) +
geom_histogram() +
ggtitle(paste("count of ", var_name))
plots[[2]] <- ggplot(train, aes_string(x = var_name, y = "SalePrice") ) +
geom_point() +
ggtitle(paste( var_name, " vs SalePrice"))
multiplot(plotlist = plots, cols = 2)
}
#构建两个绘图函数,分别可以直接输出变量名画出相对应的图像,分别是因子型变量和数值型变量。首先观察街区和房间的关系图。
plot2_factor("Neighborhood")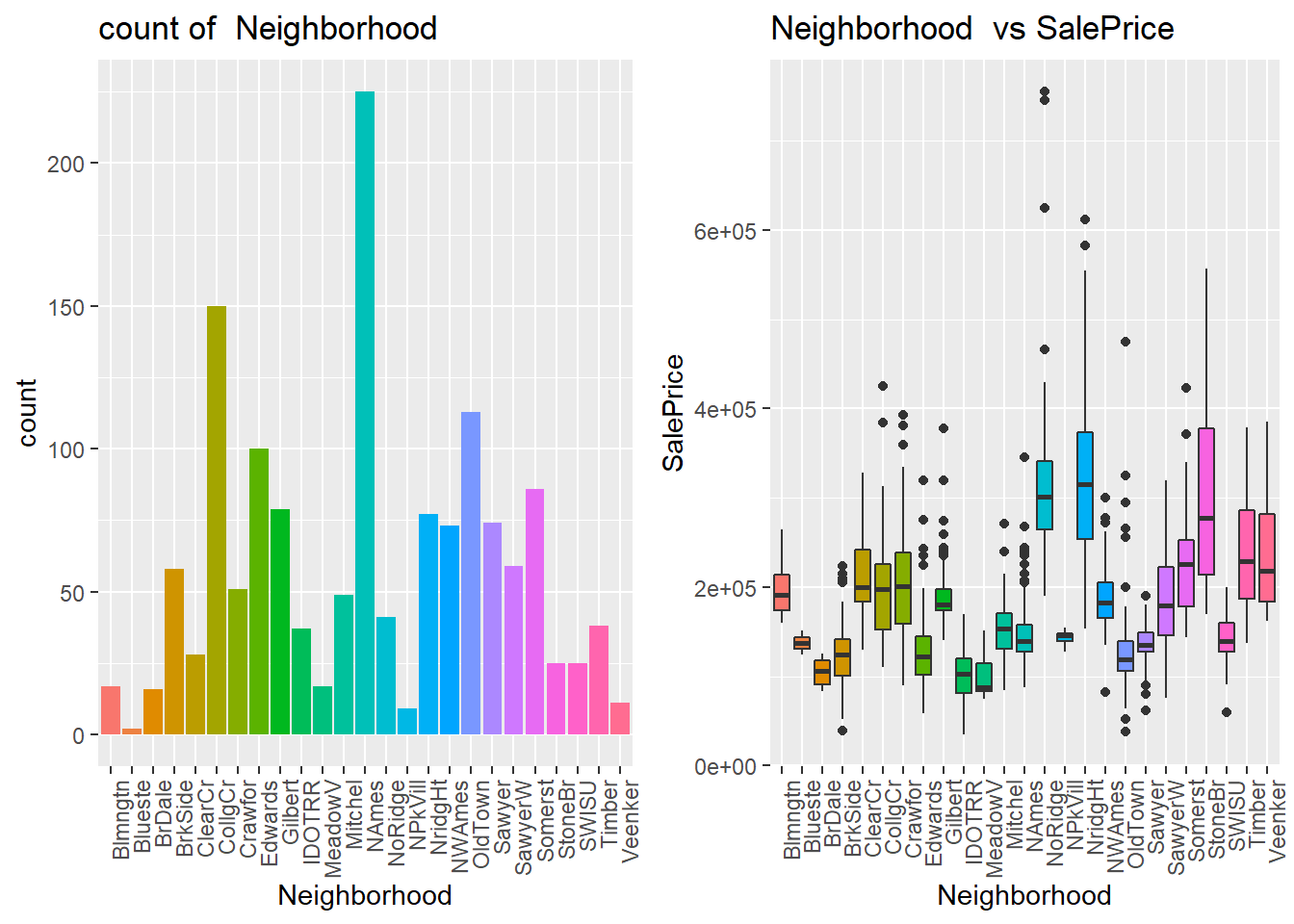
通过上图可以看出不同的社区,房价差异很大,因此这个变量应该是影响比较大的。
plot2_number("YearBuilt")## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.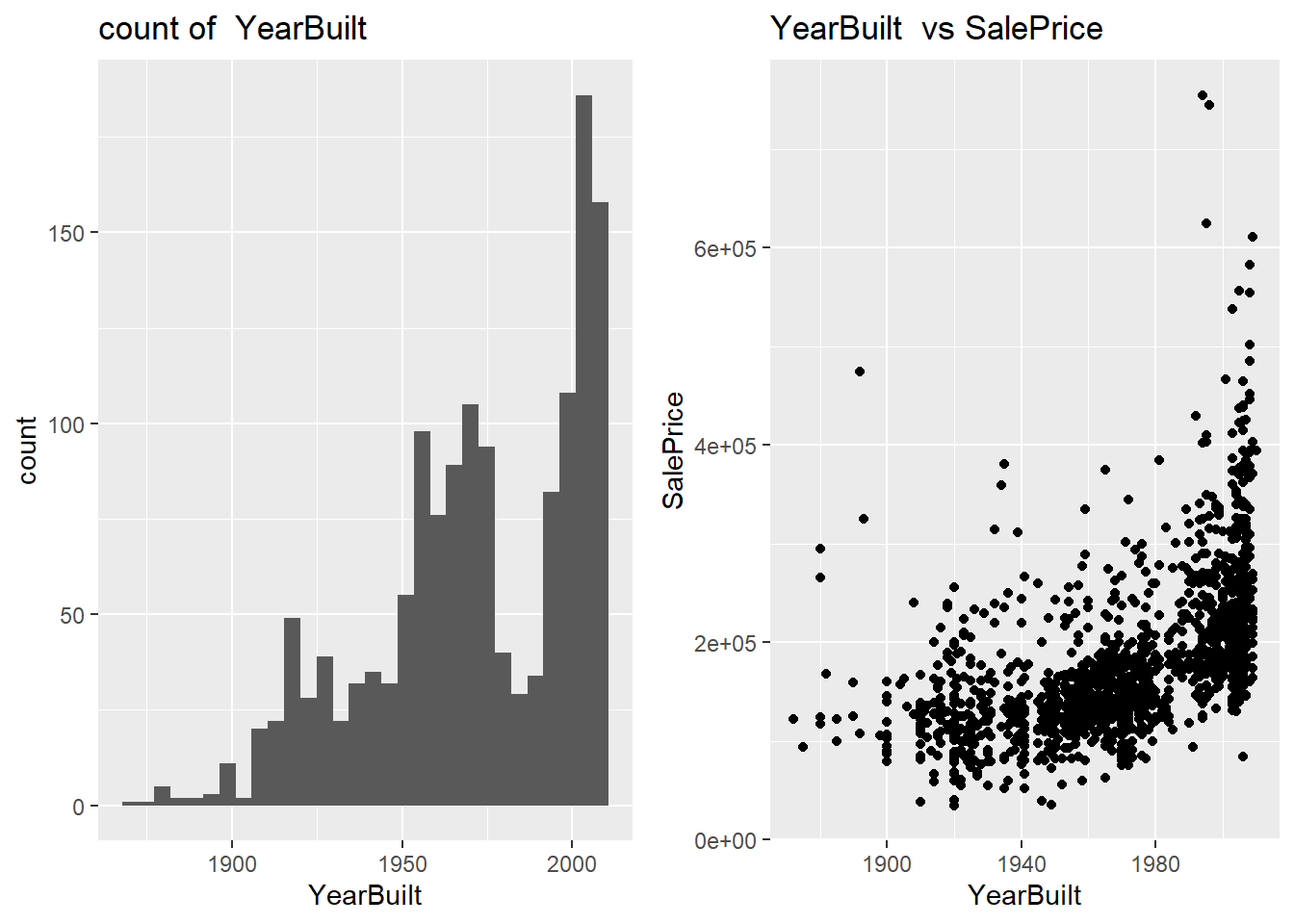
通过对建筑年限这一数值型变量进行绘图研究看出,售价和建筑年限也有强烈的线性关系,说明该变量是有意义的。
plot2_number("OverallQual")## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.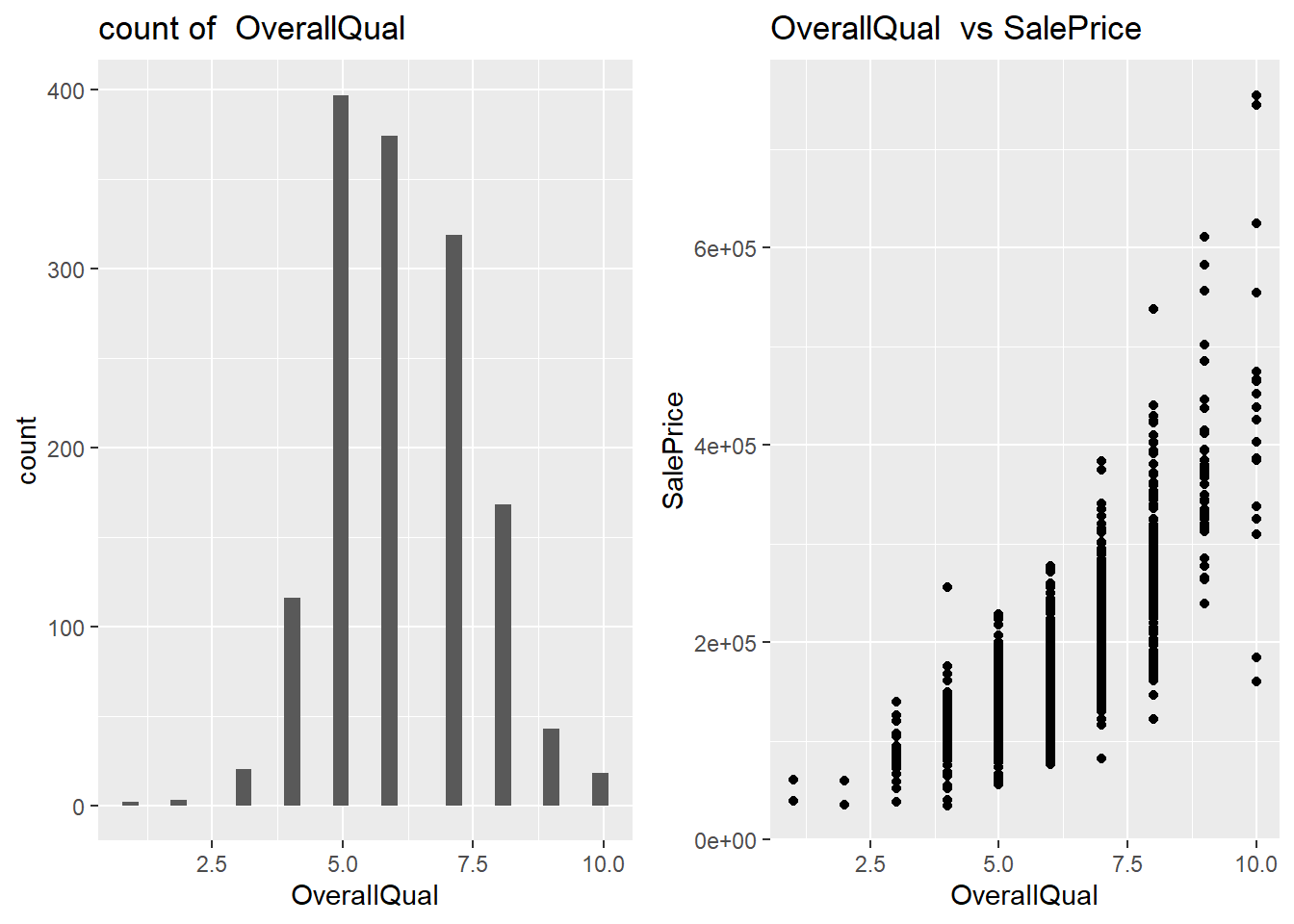
从上图看出装修越好的房子价格越高。
各个变量之间的相关性
library(corrgram)##
## 载入程辑包:'corrgram'## The following object is masked from 'package:plyr':
##
## baseball## The following object is masked from 'package:lattice':
##
## panel.fillsel <- c("LotArea","Neighborhood","BldgType","HouseStyle","YearBuilt","YearRemodAdd","OverallQual","OverallCond","MSZoning")
corrgram(train[,sel], order=TRUE, lower.panel=panel.shade, upper.panel=panel.pie, text.panel=panel.txt)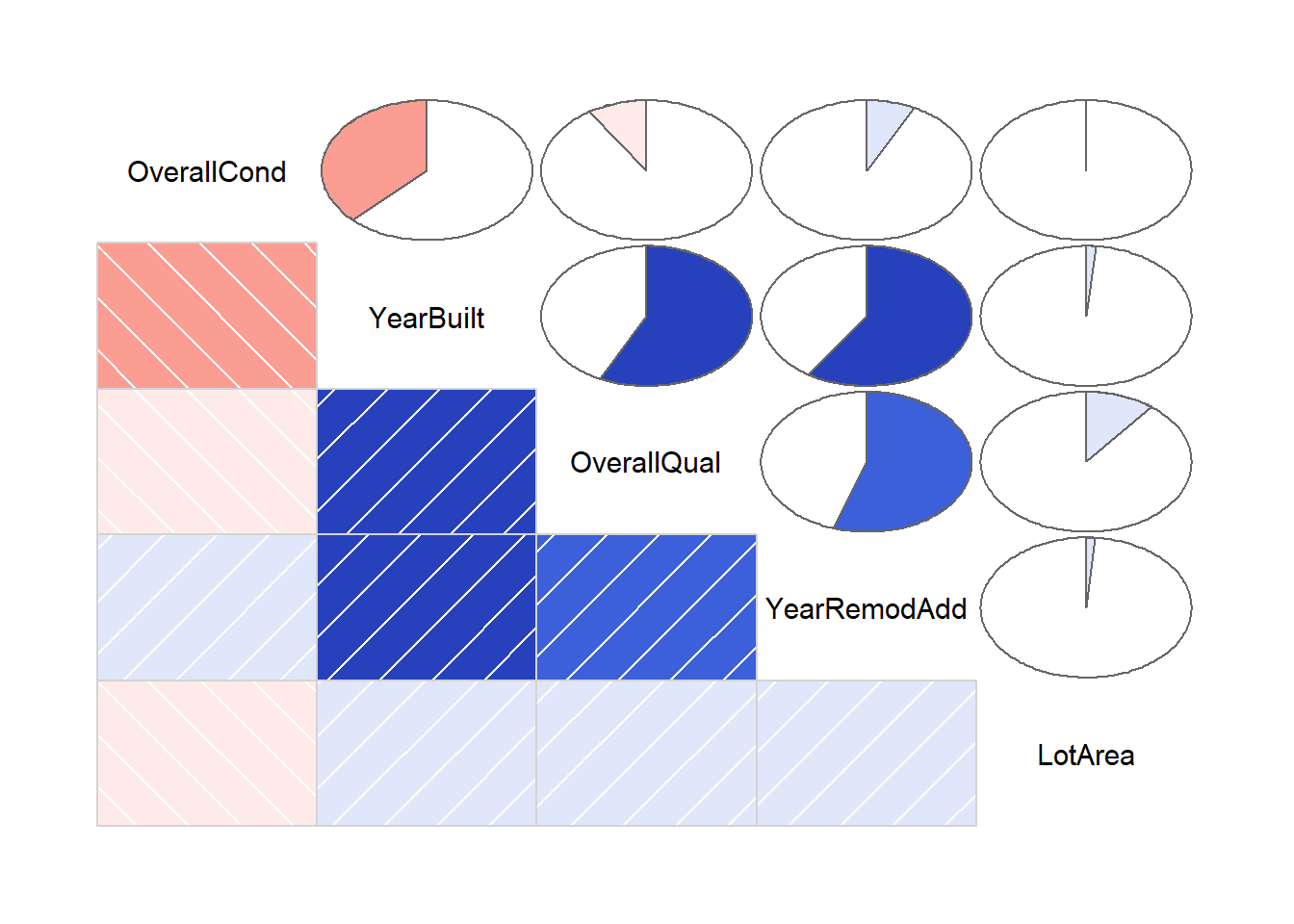
训练线性模型
tezheng <- SalePrice ~ LotArea + Neighborhood + BldgType + HouseStyle + YearBuilt + YearRemodAdd + OverallQual + OverallCond
# 训练模型
lm1 <- lm(tezheng, train)
# 查看模型概要
summary(lm1)##
## Call:
## lm(formula = tezheng, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -208970 -20882 -2917 15544 351199
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.455e+06 1.850e+05 -7.862 7.42e-15 ***
## LotArea 1.084e+00 1.156e-01 9.375 < 2e-16 ***
## NeighborhoodBlueste -1.068e+03 2.953e+04 -0.036 0.971141
## NeighborhoodBrDale -1.440e+04 1.518e+04 -0.949 0.342806
## NeighborhoodBrkSide -1.876e+04 1.278e+04 -1.468 0.142460
## NeighborhoodClearCr -2.352e+03 1.332e+04 -0.177 0.859842
## NeighborhoodCollgCr -2.917e+04 1.086e+04 -2.685 0.007335 **
## NeighborhoodCrawfor 1.747e+04 1.246e+04 1.402 0.161225
## NeighborhoodEdwards -2.813e+04 1.165e+04 -2.414 0.015924 *
## NeighborhoodGilbert -4.030e+04 1.157e+04 -3.484 0.000508 ***
## NeighborhoodIDOTRR -3.357e+04 1.343e+04 -2.499 0.012570 *
## NeighborhoodMeadowV 1.338e+04 1.446e+04 0.925 0.354867
## NeighborhoodMitchel -2.819e+04 1.196e+04 -2.356 0.018617 *
## NeighborhoodNAmes -2.202e+04 1.130e+04 -1.950 0.051426 .
## NeighborhoodNoRidge 6.105e+04 1.226e+04 4.980 7.13e-07 ***
## NeighborhoodNPkVill 6.340e+03 1.650e+04 0.384 0.700928
## NeighborhoodNridgHt 4.876e+04 1.104e+04 4.417 1.08e-05 ***
## NeighborhoodNWAmes -2.126e+04 1.166e+04 -1.823 0.068457 .
## NeighborhoodOldTown -2.915e+04 1.243e+04 -2.344 0.019194 *
## NeighborhoodSawyer -2.575e+04 1.188e+04 -2.168 0.030350 *
## NeighborhoodSawyerW -2.224e+04 1.154e+04 -1.927 0.054234 .
## NeighborhoodSomerst -1.228e+04 1.093e+04 -1.123 0.261764
## NeighborhoodStoneBr 5.984e+04 1.249e+04 4.790 1.84e-06 ***
## NeighborhoodSWISU -2.365e+04 1.433e+04 -1.651 0.099024 .
## NeighborhoodTimber -1.326e+04 1.236e+04 -1.073 0.283489
## NeighborhoodVeenker 2.303e+04 1.555e+04 1.481 0.138905
## BldgType2fmCon 1.230e+03 7.413e+03 0.166 0.868218
## BldgTypeDuplex -7.231e+02 5.831e+03 -0.124 0.901330
## BldgTypeTwnhs -6.675e+04 7.811e+03 -8.546 < 2e-16 ***
## BldgTypeTwnhsE -4.916e+04 4.892e+03 -10.049 < 2e-16 ***
## HouseStyle1.5Unf -2.835e+04 1.102e+04 -2.573 0.010184 *
## HouseStyle1Story -3.981e+03 3.977e+03 -1.001 0.316972
## HouseStyle2.5Fin 5.328e+04 1.472e+04 3.619 0.000306 ***
## HouseStyle2.5Unf -4.606e+03 1.250e+04 -0.368 0.712613
## HouseStyle2Story 4.069e+03 4.205e+03 0.968 0.333393
## HouseStyleSFoyer -1.173e+04 7.791e+03 -1.505 0.132424
## HouseStyleSLvl -6.438e+03 6.197e+03 -1.039 0.299077
## YearBuilt 4.285e+02 8.428e+01 5.084 4.20e-07 ***
## YearRemodAdd 3.114e+02 7.505e+01 4.149 3.53e-05 ***
## OverallQual 2.849e+04 1.187e+03 24.010 < 2e-16 ***
## OverallCond 1.613e+03 1.150e+03 1.402 0.161035
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 38880 on 1419 degrees of freedom
## Multiple R-squared: 0.7671, Adjusted R-squared: 0.7605
## F-statistic: 116.8 on 40 and 1419 DF, p-value: < 2.2e-16模型中部分特征没有显著,但是模型整体的F检验通过,说明该模型还是可以的。模型调整后的\(R^2=0.7605\)效果还不错。
变量选择
首先进行人工变量选择,去除不显著的变量。去掉OverallCond,重新进行拟合
# 初步决定的 lm.base 模型的变量
fm.base <- SalePrice ~ LotArea + Neighborhood + BldgType + HouseStyle + YearBuilt + YearRemodAdd + OverallQual
# 训练模型
lm.base <- lm(fm.base, train)
summary(lm.base)##
## Call:
## lm(formula = fm.base, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -209817 -20321 -2822 15210 352218
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.464e+06 1.850e+05 -7.914 4.98e-15 ***
## LotArea 1.081e+00 1.156e-01 9.352 < 2e-16 ***
## NeighborhoodBlueste 7.266e+02 2.951e+04 0.025 0.980358
## NeighborhoodBrDale -1.362e+04 1.517e+04 -0.898 0.369408
## NeighborhoodBrkSide -1.798e+04 1.277e+04 -1.408 0.159440
## NeighborhoodClearCr -1.805e+03 1.331e+04 -0.136 0.892207
## NeighborhoodCollgCr -2.898e+04 1.087e+04 -2.667 0.007744 **
## NeighborhoodCrawfor 1.883e+04 1.243e+04 1.516 0.129852
## NeighborhoodEdwards -2.782e+04 1.166e+04 -2.387 0.017109 *
## NeighborhoodGilbert -4.028e+04 1.157e+04 -3.481 0.000515 ***
## NeighborhoodIDOTRR -3.359e+04 1.344e+04 -2.499 0.012553 *
## NeighborhoodMeadowV 1.425e+04 1.445e+04 0.986 0.324151
## NeighborhoodMitchel -2.759e+04 1.196e+04 -2.307 0.021210 *
## NeighborhoodNAmes -2.091e+04 1.127e+04 -1.855 0.063807 .
## NeighborhoodNoRidge 6.106e+04 1.226e+04 4.980 7.14e-07 ***
## NeighborhoodNPkVill 7.526e+03 1.649e+04 0.456 0.648117
## NeighborhoodNridgHt 4.836e+04 1.104e+04 4.380 1.27e-05 ***
## NeighborhoodNWAmes -1.993e+04 1.163e+04 -1.714 0.086670 .
## NeighborhoodOldTown -2.849e+04 1.243e+04 -2.292 0.022025 *
## NeighborhoodSawyer -2.475e+04 1.186e+04 -2.086 0.037120 *
## NeighborhoodSawyerW -2.201e+04 1.155e+04 -1.907 0.056764 .
## NeighborhoodSomerst -1.248e+04 1.094e+04 -1.141 0.254229
## NeighborhoodStoneBr 5.963e+04 1.250e+04 4.772 2.01e-06 ***
## NeighborhoodSWISU -2.346e+04 1.433e+04 -1.637 0.101780
## NeighborhoodTimber -1.325e+04 1.236e+04 -1.072 0.283915
## NeighborhoodVeenker 2.475e+04 1.551e+04 1.596 0.110733
## BldgType2fmCon 7.637e+02 7.408e+03 0.103 0.917900
## BldgTypeDuplex -1.566e+03 5.802e+03 -0.270 0.787285
## BldgTypeTwnhs -6.658e+04 7.813e+03 -8.522 < 2e-16 ***
## BldgTypeTwnhsE -4.951e+04 4.888e+03 -10.129 < 2e-16 ***
## HouseStyle1.5Unf -2.800e+04 1.102e+04 -2.541 0.011173 *
## HouseStyle1Story -4.114e+03 3.977e+03 -1.035 0.301043
## HouseStyle2.5Fin 5.310e+04 1.473e+04 3.606 0.000322 ***
## HouseStyle2.5Unf -5.807e+03 1.248e+04 -0.465 0.641658
## HouseStyle2Story 3.910e+03 4.205e+03 0.930 0.352516
## HouseStyleSFoyer -1.110e+04 7.781e+03 -1.427 0.153881
## HouseStyleSLvl -6.096e+03 6.195e+03 -0.984 0.325288
## YearBuilt 3.934e+02 8.052e+01 4.886 1.15e-06 ***
## YearRemodAdd 3.548e+02 6.840e+01 5.186 2.46e-07 ***
## OverallQual 2.863e+04 1.183e+03 24.206 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 38890 on 1420 degrees of freedom
## Multiple R-squared: 0.7668, Adjusted R-squared: 0.7603
## F-statistic: 119.7 on 39 and 1420 DF, p-value: < 2.2e-16发现模型的效果没有显著提升。
变量选择方法
传统的变量选择方法有很多,例如LASSO,Ridge等方法,这里我们使用Lasso,随机森林和梯度下降法来进行变量选择,提升模型性能。
# 安装
library(glmnet)## 载入需要的程辑包:Matrix## Loaded glmnet 4.1-1# 准备数据
formula <- as.formula( log(SalePrice)~ .-Id )
# model.matrix 会自动将分类变量变成哑变量
x <- model.matrix(formula, train)
y <- log(train$SalePrice)
#执行 lasso
set.seed(999)
lm.lasso <- cv.glmnet(x, y, alpha=1)
# 画图
plot(lm.lasso)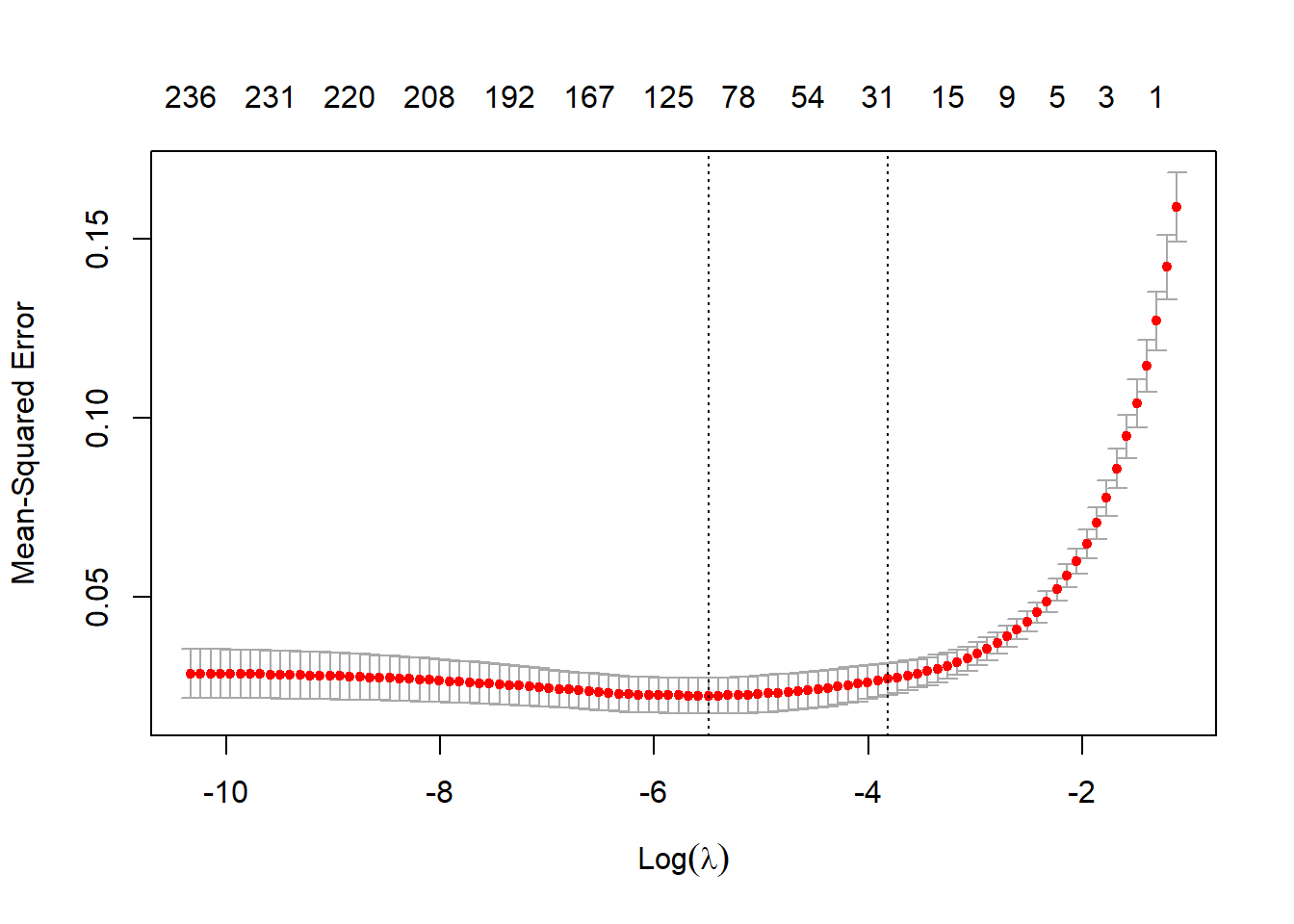
# 得到各变量的系数
coef(lm.lasso, s = "lambda.min")## 242 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 7.314346e+00
## (Intercept) .
## MSSubClass -3.089056e-04
## MSZoningFV 1.793795e-02
## MSZoningRH .
## MSZoningRL 4.132766e-02
## MSZoningRM .
## LotFrontage .
## LotArea 1.272041e-06
## StreetPave 4.921358e-02
## LotShapeIR2 1.071380e-02
## LotShapeIR3 -9.683435e-02
## LotShapeReg .
## LandContourHLS .
## LandContourLow .
## LandContourLvl .
## LotConfigCulDSac 3.543690e-02
## LotConfigFR2 .
## LotConfigFR3 .
## LotConfigInside .
## LandSlopeMod .
## LandSlopeSev .
## NeighborhoodBlueste .
## NeighborhoodBrDale -1.493220e-02
## NeighborhoodBrkSide .
## NeighborhoodClearCr 3.747801e-02
## NeighborhoodCollgCr .
## NeighborhoodCrawfor 1.115702e-01
## NeighborhoodEdwards -4.439143e-02
## NeighborhoodGilbert .
## NeighborhoodIDOTRR -6.746018e-02
## NeighborhoodMeadowV -7.649854e-02
## NeighborhoodMitchel .
## NeighborhoodNAmes .
## NeighborhoodNoRidge 5.440480e-02
## NeighborhoodNPkVill .
## NeighborhoodNridgHt 1.179915e-01
## NeighborhoodNWAmes .
## NeighborhoodOldTown -2.833497e-02
## NeighborhoodSawyer .
## NeighborhoodSawyerW .
## NeighborhoodSomerst 6.349095e-02
## NeighborhoodStoneBr 1.204762e-01
## NeighborhoodSWISU .
## NeighborhoodTimber 2.260192e-03
## NeighborhoodVeenker 2.878460e-02
## Condition1Feedr -1.568548e-02
## Condition1Norm 3.532074e-02
## Condition1PosA .
## Condition1PosN .
## Condition1RRAe -2.434992e-02
## Condition1RRAn .
## Condition1RRNe .
## Condition1RRNn .
## Condition2Feedr .
## Condition2Norm .
## Condition2PosA .
## Condition2PosN -5.253862e-01
## Condition2RRAe .
## Condition2RRAn .
## Condition2RRNn .
## BldgType2fmCon .
## BldgTypeDuplex .
## BldgTypeTwnhs -7.598136e-02
## BldgTypeTwnhsE -1.805548e-02
## HouseStyle1.5Unf .
## HouseStyle1Story .
## HouseStyle2.5Fin .
## HouseStyle2.5Unf .
## HouseStyle2Story .
## HouseStyleSFoyer .
## HouseStyleSLvl .
## OverallQual 6.845347e-02
## OverallCond 3.219936e-02
## YearBuilt 1.274539e-03
## YearRemodAdd 8.437361e-04
## RoofStyleGable -5.642072e-03
## RoofStyleGambrel .
## RoofStyleHip .
## RoofStyleMansard .
## RoofStyleShed .
## RoofMatlCompShg 8.744853e-03
## RoofMatlMembran .
## RoofMatlMetal .
## RoofMatlRoll .
## RoofMatlTar&Grv .
## RoofMatlWdShake .
## RoofMatlWdShngl 7.458154e-02
## Exterior1stAsphShn .
## Exterior1stBrkComm -1.345774e-01
## Exterior1stBrkFace 4.770749e-02
## Exterior1stCBlock .
## Exterior1stCemntBd .
## Exterior1stHdBoard -8.584669e-03
## Exterior1stImStucc .
## Exterior1stMetalSd .
## Exterior1stPlywood .
## Exterior1stStone .
## Exterior1stStucco .
## Exterior1stVinylSd .
## Exterior1stWd Sdng -6.333826e-03
## Exterior1stWdShing .
## Exterior2ndAsphShn .
## Exterior2ndBrk Cmn .
## Exterior2ndBrkFace .
## Exterior2ndCBlock .
## Exterior2ndCmentBd 1.903051e-03
## Exterior2ndHdBoard .
## Exterior2ndImStucc .
## Exterior2ndMetalSd .
## Exterior2ndOther .
## Exterior2ndPlywood .
## Exterior2ndStone .
## Exterior2ndStucco -4.652564e-02
## Exterior2ndVinylSd .
## Exterior2ndWd Sdng .
## Exterior2ndWd Shng -1.387069e-02
## MasVnrTypeBrkFace .
## MasVnrTypeNone .
## MasVnrTypeStone .
## MasVnrArea .
## ExterQualFa -1.044328e-02
## ExterQualGd .
## ExterQualTA -6.848606e-03
## ExterCondFa -9.876932e-03
## ExterCondGd .
## ExterCondPo .
## ExterCondTA 4.288596e-03
## FoundationCBlock .
## FoundationPConc 2.610683e-02
## FoundationSlab -2.033377e-03
## FoundationStone .
## FoundationWood .
## BsmtQualFa .
## BsmtQualGd .
## BsmtQualTA -2.813238e-04
## BsmtQualNone -3.399457e-03
## BsmtCondGd .
## BsmtCondPo .
## BsmtCondTA 3.624419e-03
## BsmtCondNone .
## BsmtExposureGd 4.858853e-02
## BsmtExposureMn .
## BsmtExposureNo -6.556593e-03
## BsmtExposureNone -3.795778e-02
## BsmtFinType1BLQ .
## BsmtFinType1GLQ 9.606824e-03
## BsmtFinType1LwQ .
## BsmtFinType1Rec .
## BsmtFinType1Unf -3.321896e-02
## BsmtFinType1None .
## BsmtFinSF1 .
## BsmtFinType2BLQ -7.694026e-03
## BsmtFinType2GLQ .
## BsmtFinType2LwQ .
## BsmtFinType2Rec .
## BsmtFinType2Unf .
## BsmtFinType2None -2.374994e-02
## BsmtFinSF2 .
## BsmtUnfSF .
## TotalBsmtSF 2.725149e-05
## HeatingGasA .
## HeatingGasW 6.541262e-02
## HeatingGrav -1.079210e-01
## HeatingOthW .
## HeatingWall .
## HeatingQCFa .
## HeatingQCGd -2.803107e-03
## HeatingQCPo .
## HeatingQCTA -1.893740e-02
## CentralAirY 6.505505e-02
## ElectricalFuseF .
## ElectricalFuseP .
## ElectricalMix .
## ElectricalSBrkr .
## X1stFlrSF 2.739845e-05
## X2ndFlrSF .
## LowQualFinSF .
## GrLivArea 1.960863e-04
## BsmtFullBath 4.369629e-02
## BsmtHalfBath .
## FullBath 2.498523e-02
## HalfBath 1.102765e-02
## BedroomAbvGr .
## KitchenAbvGr -2.694865e-02
## KitchenQualFa .
## KitchenQualGd .
## KitchenQualTA -7.346020e-03
## TotRmsAbvGrd 8.445023e-03
## FunctionalMaj2 -1.661537e-01
## FunctionalMin1 .
## FunctionalMin2 .
## FunctionalMod .
## FunctionalSev -1.691674e-01
## FunctionalTyp 3.674019e-02
## Fireplaces 2.925835e-02
## GarageTypeAttchd 1.017935e-02
## GarageTypeBasment -2.805227e-04
## GarageTypeBuiltIn .
## GarageTypeCarPort .
## GarageTypeDetchd .
## GarageTypeNone -5.483381e-04
## GarageYrBlt .
## GarageFinishRFn .
## GarageFinishUnf -3.452388e-03
## GarageFinishNone -6.132096e-05
## GarageCars 5.606530e-02
## GarageArea 3.428652e-05
## GarageQualFa -9.605669e-03
## GarageQualGd 1.663474e-02
## GarageQualPo .
## GarageQualTA .
## GarageQualNone -2.467408e-04
## GarageCondFa -1.397724e-02
## GarageCondGd .
## GarageCondPo .
## GarageCondTA .
## GarageCondNone -2.685390e-06
## PavedDriveP .
## PavedDriveY 1.160351e-02
## WoodDeckSF 9.033916e-05
## OpenPorchSF .
## EnclosedPorch 2.864247e-06
## X3SsnPorch 1.227765e-05
## ScreenPorch 2.102909e-04
## PoolArea -6.262337e-05
## MiscVal .
## MoSold .
## YrSold -4.603035e-04
## SaleTypeCon .
## SaleTypeConLD .
## SaleTypeConLI .
## SaleTypeConLw .
## SaleTypeCWD .
## SaleTypeNew 7.765443e-02
## SaleTypeOth .
## SaleTypeWD .
## SaleConditionAdjLand .
## SaleConditionAlloca .
## SaleConditionFamily .
## SaleConditionNormal 3.497182e-02
## SaleConditionPartial .#由于 SalePrice 为 NA 无法数组化
test$SalePrice <- 1
test_x <- model.matrix(formula, test)
# 预测、输出结果
lm.pred <- predict(lm.lasso, newx = test_x, s = "lambda.min")
res <- data.frame(Id = test$Id, SalePrice = exp(lm.pred))
write.csv(res, file = "res_lasso.csv", row.names = FALSE)使用随机森林方法进行回归建模.
library(randomForest)
library(caret)
#设定种子
set.seed(223)
# 设定控制参数
# method = "cv" -- k 折交叉验证
# number -- K 折交叉验证中的 K, number=10 则是 10 折交叉验证
# repeats -- 交叉验证的次数
# verboseIter -- 打印训练日志
ctrl <- trainControl(method = "cv", number = 10, repeats = 20, verboseIter = TRUE)
# 训练模型
lm.rf <- train(log(SalePrice)~ .-Id, data = train, method = "rf", trControl = ctrl, tuneLength = 3)
# 输出结果
#write_res(lm.rf, test, 'rf')
# 输出结果
lm.pred <- predict(lm.rf, test)
res <- data.frame(Id = test$Id, SalePrice = exp(lm.pred))
write.csv(res, file = "res_rf.csv", row.names = FALSE)使用梯度下降法进行模型建立。
lm.gbm <- train(log(SalePrice)~ .-Id, data = train, method = "gbm", trControl = ctrl)
# 输出结果
lm.pred <- predict(lm.gbm, test)
res <- data.frame(Id = test$Id, SalePrice = exp(lm.pred))
write.csv(res, file = "res_gbm.csv", row.names = FALSE)最终我们得到了各个方法进行预测的残差,并且进行计算得到了各个方法的RES值,通过对比可以得出相对最好的方法,想要进一步提升模型的性能,可以使用bagging,stacking等模型融合的方法来进行改进。
使用BeSS方法进行变量选择回归。
之前使用的是比较传统的方法,这里本文使用最优子集法,使用BeSS包对该问题进行分析建模。
最优子集法即best subset selection,最早可见Hocking[@hocking1967selection]等人1967年的文章,其思想十分简单。从零号模型(null model)\(M_0\)开始,这个模型只有截距项而没有任何自变量。然后用不同的特征组合进行拟合,从特征中分别挑选出一个最好的模型(RSS最小或\(R^2\)最大),也就是包含1个特征的模型\(M_1\),包含2个特征的模型\(M_2\),直至包含p个特征的模型\(M_p\)。然后从这总共p+1个模型中选出其中最好的模型(根据交叉验证误差,\(C_p\),BIC或adjusted \(R^2\))(注:为什么不能用RSS或\(R^2\)来衡量?因为增加任何特征,模型的训练RSS只会变小,\(R^2\)只会增大)。这个最好模型所配置的特征就是筛选出的特征。最优子集法在理想的条件下可以筛选出最好的特征集合出来,但是其高昂的计算成本是阻碍其应用的主要问题。Zhu[@Zhu2021]等人在2021年提出了一种最优子集法的多项式算法,证明了在一定条件下,该算法具有以下三个优良性质:
- 计算复杂度是多项式的
- 选择出来的子集能够覆盖真实的集合
- 该算法的解是全局最优的
作者将该方法称为Adaptive Best-Subset Selection以下简称BeSS,在作者提出的SIC(special information criterion)准则下,该方法的模型选择连续性得到了证明。SIC准则如下: \[\operatorname{SIC}(\mathcal{A})=n \log \mathcal{L}_{\mathcal{A}}+|\mathcal{A}| \log (p) \log \log n\] 其中\(\mathcal{A}\)为筛选出来的特征的集合。
剪接方法简介
首先定义一些变量名称,\(\boldsymbol{\beta}=\left(\beta_{1}, \ldots, \beta_{p}\right)^{\top} \in \mathbb{R}^{p}\),将\(\ell_{q}\)定义为:\(\|\boldsymbol{\beta}\|_{q}=\left(\sum_{j=1}^{p}\left|\beta_{j}\right|^{q}\right)^{1 / q},q \in[1, \infty)\)。\(\mathcal{S}=\{1, \ldots, p\}\),对任何\(\mathcal{A} \subseteq \mathcal{S}\),记\(\mathcal{A}^{c}=\mathcal{S} \backslash \mathcal{A}\)作为\(\mathcal{A}\)的补集,\(|\mathcal{A}|\)作为他的基。将\(\beta\)的子集定义为\(\operatorname{supp}(\boldsymbol{\beta})=\left\{j: \beta_{j} \neq 0\right\}\)。对一个指标集\(\mathcal{A} \subseteq\{1, \ldots, p\}\),\(\boldsymbol{\beta}_{\mathcal{A}}=\left(\beta_{j}, j \in \mathcal{A}\right) \in \mathbb{R}^{|\mathcal{A}|}\)。对一个矩阵\(\boldsymbol{X} \in \mathbb{R}^{n \times p}\)定义\(\boldsymbol{X}_{\mathcal{A}} =(X_{j},j \in \mathcal{A}) \in \mathbb{R}^{n \times|\mathcal{A}|}\)。对任何一个向量\(t\)和任何一个集合\(\mathcal{A}\),\(t^{\mathcal{A}}\)是一个第\(j\)个元素\(\left(\boldsymbol{t}^{\mathcal{A}}\right)_{j}\)如果\(j \in \mathcal{A}\)就等于\(t_{j}\),否则为0。
在文章中,作者最重要的贡献是提出了剪接方法,即splicing method,通过使用该种方法,显著的提升了最优子集算法的性能,使其在当前的环境下变的可行。 考虑\(\ell_{0}\)限制最小化问题:\[
\min _{\boldsymbol{\beta}} \mathcal{L}_{n}(\boldsymbol{\beta}), \quad \text { s. } t\|\boldsymbol{\beta}\|_{0} \leq \boldsymbol{s}
\] 其中:\(\mathcal{L}_{n}(\boldsymbol{\beta})=\frac{1}{2 n}\|\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta}\|_{2}^{2}\)。在不考虑全局损失的情况下,我们考虑\(\|\boldsymbol{\beta}\|_{0}=\boldsymbol{s}\)。给定一个初始集合\(\mathcal{A} \subset \mathcal{S}=\{1,2, \ldots, p\}\),且\(|\mathcal{A}|=s\),记\(\mathcal{I}=\mathcal{A}^{c}\)并且计算\[
\hat{\boldsymbol{\beta}}=\arg \min _{\boldsymbol{\beta}_{\mathcal{I}}=0} \mathcal{L}_{n}(\boldsymbol{\beta})
\] 将\(\mathcal{A}\)和\(\mathcal{I}\)定义为激活集合和非激活集合,这里的激活就是在真实集合中的意思。在给定了\(\mathcal{A}\)和\(\hat{\beta}\)之后,可以定义两种损失如下:
后退损失\[ \xi_{j}=\mathcal{L}_{n}\left(\hat{\boldsymbol{\beta}}^{\mathcal{A} \backslash\{j\}}\right)-\mathcal{L}_{n}\left(\hat{\boldsymbol{\beta}}^{\mathcal{A}}\right)=\frac{\boldsymbol{X}_{j}^{\top} \boldsymbol{X}_{j}}{2 n}\left(\hat{\beta}_{j}\right)^{2} \]
前进损失:\[ \zeta_{j}=\mathcal{L}_{n}\left(\hat{\boldsymbol{\beta}}^{\mathcal{A}}\right)-\mathcal{L}_{n}\left(\hat{\boldsymbol{\beta}}^{\mathcal{A}}+\hat{\boldsymbol{t}}^{\{j\}}\right)=\frac{\boldsymbol{X}_{j}^{\top} \boldsymbol{X}_{j}}{2 n}\left(\frac{\hat{d}_{j}}{\boldsymbol{X}_{j}^{\top} \boldsymbol{X}_{j} / n}\right)^{2} \] 其中:\(\hat{t}=\arg \min _{t} \mathcal{L}_{n}\left(\hat{\boldsymbol{\beta}}^{\mathcal{A}}+\boldsymbol{t}^{\{j\}}\right), \hat{d}_{j}=\boldsymbol{X}_{j}^{\top}(\boldsymbol{y}-\boldsymbol{X} \hat{\boldsymbol{\beta}}) / n\)
直观的而言,对\(j \in \mathcal{A}\)一个大的\(\xi_{j}\)说明这个变量是潜在重要的。但是由于子集大小不同,这两个损失是无法比较的。然而如果将\(\mathcal{A}\)中的一些不是那么相关的变量和\(\mathcal{I}\)中一些重要的变量交换,这也许能够获得比较好的结果,这就是剪接法的思想所在。 特别的,对任何给定的\(k <= s\)定义如下: \[ \mathcal{A}_{k}=\left\{j \in \mathcal{A}: \sum_{i \in \mathcal{A}} \mathrm{I}\left(\xi_{j} \geq \xi_{i}\right) \leq k\right\} \] \[ \mathcal{I}_{k}=\left\{j \in \mathcal{I}: \sum_{i \in \mathcal{I}} \mathrm{I}\left(\zeta_{j} \leq \zeta_{i}\right) \leq k\right\} \] 通过交换\(\mathcal{A}_{k}\)和\(\mathcal{I}_{k}\),从而实现对\(\mathcal{A}\)和\(\mathcal{I}\)的切片,得到了新的集合: \[ \tilde{\mathcal{A}}=\left(\mathcal{A} \backslash \mathcal{A}_{k}\right) \cup \mathcal{I}_{k} \] 记\(\tilde{\mathcal{I}}=\tilde{\mathcal{A}}^{c}, \tilde{\boldsymbol{\beta}}=\arg \min _{\boldsymbol{\beta}_{\tilde{\mathcal{I}}}=0} \mathcal{L}_{n}(\boldsymbol{\beta})\),并且\(\tau_{s}>0\)为阈值。如果\(\tau_{s} < \mathcal{L}_{n}(\hat{\boldsymbol{\beta}})-\mathcal{L}_{n}(\tilde{\boldsymbol{\beta}})\) 则说明\(\tilde{\mathcal{A}}\)是优于\(\mathcal{A}\)。通过这样的方法则可以更新集合\(\mathcal{A}\)指导损失函数不能够通过剪接方法来进行提升。还有的问题就是设定初始集。通常来说我们选定第一批\(s\)个特征,这些特征是与\(y\)关联程度最大的特征。设\(k_{max}\)为剪接最大尺寸,\(k_{max}<s\),接下来的算法演示了如何计算具体的方法。
# 这里使用之前构造好的x矩阵,将分类因子型变量转化为哑变量
library(BeSS)
bessmodel<-bess(x,log(train$SalePrice),family = "gaussian",K.max = 40,max.steps = 30,method = "gsection")## 1-th iteration s.left:1 s.split:124 s.right:200
## 2-th iteration s.left:1 s.split:77 s.right:124
## 3-th iteration s.left:77 s.split:106 s.right:124
## 4-th iteration s.left:77 s.split:95 s.right:106
## 5-th iteration s.left:95 s.split:102 s.right:106
## 6-th iteration s.left:102 s.split:104 s.right:106
## 7-th iteration s.left:104 s.split:105 s.right:106plot(bessmodel,type = "both",breaks = TRUE,K=10)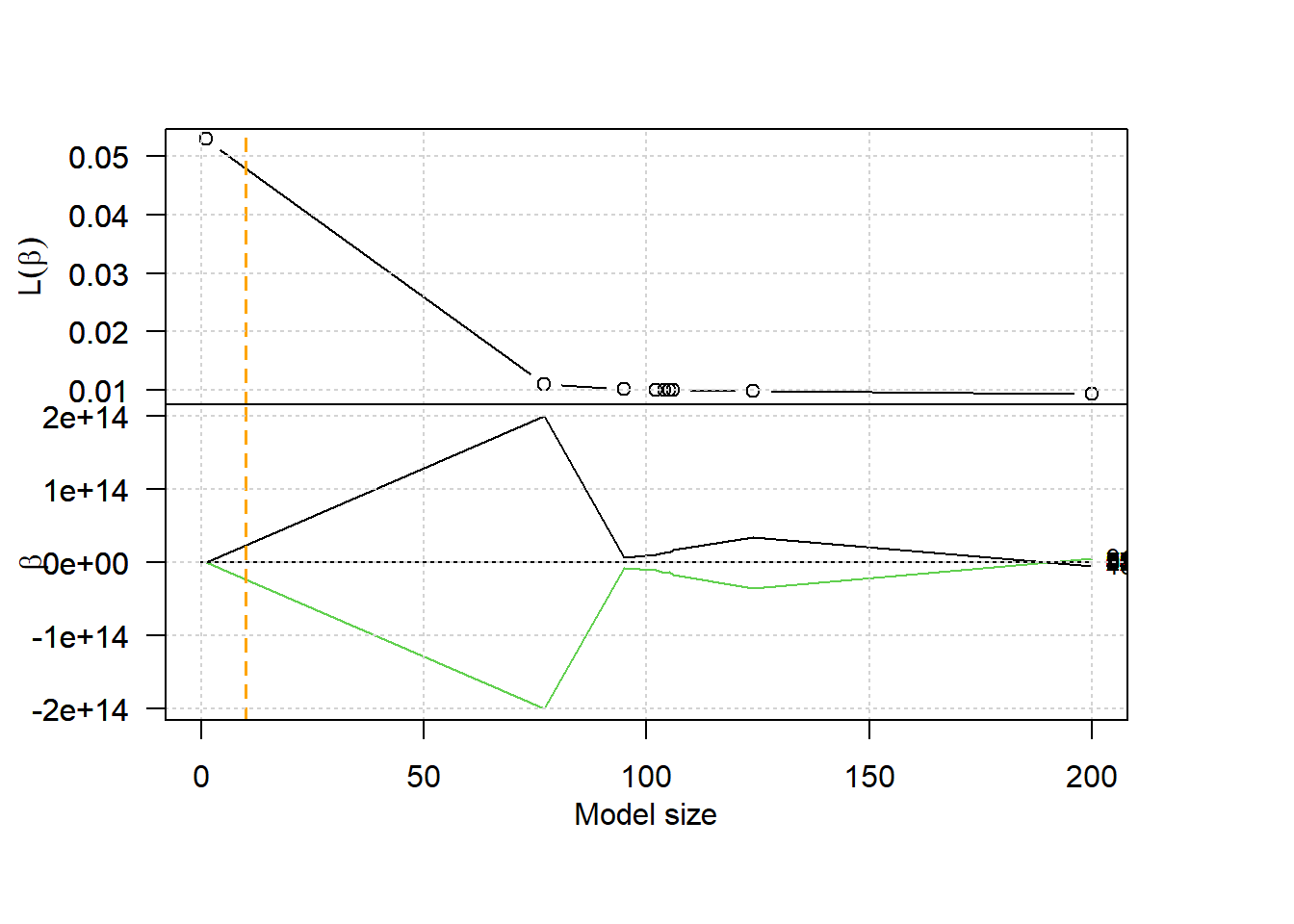
bessmodel## Df MSE AIC BIC EBIC
## [1,] 1 0.052971658 -4287.477 -4282.191 -4271.222
## [2,] 200 0.009208594 -6443.922 -5386.684 -3192.765
## [3,] 124 0.009723193 -6516.532 -5861.044 -4500.815
## [4,] 77 0.010871005 -6447.618 -6040.581 -5195.922
## [5,] 106 0.009944842 -6519.624 -5959.288 -4796.511
## [6,] 95 0.010160562 -6510.293 -6008.104 -4965.993
## [7,] 102 0.010012268 -6517.758 -5978.567 -4859.668
## [8,] 104 0.009982011 -6518.177 -5968.413 -4827.575
## [9,] 105 0.009951605 -6520.631 -5965.581 -4813.774输出使用bess方法建立的最优模型
bestmodel<-bessmodel$bestmodel
summary(bestmodel)##
## Call:
## lm(formula = ys ~ xbest, weights = weights)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.75141 -0.05143 0.00246 0.05453 0.75141
##
## Coefficients: (2 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.630e+00 5.931e-01 2.749 0.006061 **
## xbestMSSubClass -2.562e-04 1.032e-04 -2.482 0.013169 *
## xbestMSZoningFV 4.833e-01 3.969e-02 12.176 < 2e-16 ***
## xbestMSZoningRH 4.325e-01 4.437e-02 9.749 < 2e-16 ***
## xbestMSZoningRL 4.287e-01 3.681e-02 11.646 < 2e-16 ***
## xbestMSZoningRM 3.635e-01 3.676e-02 9.890 < 2e-16 ***
## xbestLotFrontage 5.194e-04 1.748e-04 2.971 0.003019 **
## xbestLotArea 2.768e-06 4.207e-07 6.579 6.73e-11 ***
## xbestLotShapeIR2 2.952e-02 1.778e-02 1.660 0.097089 .
## xbestLotConfigCulDSac 4.148e-02 1.237e-02 3.353 0.000822 ***
## xbestLandSlopeSev -2.262e-01 4.596e-02 -4.921 9.66e-07 ***
## xbestNeighborhoodBrkSide 4.672e-02 1.579e-02 2.960 0.003134 **
## xbestNeighborhoodCrawfor 1.276e-01 1.697e-02 7.518 1.00e-13 ***
## xbestNeighborhoodEdwards -5.667e-02 1.285e-02 -4.412 1.11e-05 ***
## xbestNeighborhoodMeadowV -1.291e-01 3.391e-02 -3.808 0.000146 ***
## xbestNeighborhoodMitchel -3.483e-02 1.626e-02 -2.142 0.032354 *
## xbestNeighborhoodNAmes -1.736e-02 9.775e-03 -1.776 0.075923 .
## xbestNeighborhoodNoRidge 3.049e-02 1.902e-02 1.603 0.109270
## xbestNeighborhoodNridgHt 7.814e-02 1.559e-02 5.012 6.10e-07 ***
## xbestNeighborhoodStoneBr 1.220e-01 2.347e-02 5.197 2.34e-07 ***
## xbestCondition1Norm 5.229e-02 9.153e-03 5.713 1.37e-08 ***
## xbestCondition1PosN 4.631e-02 2.784e-02 1.664 0.096435 .
## xbestCondition1RRAe -6.459e-02 3.342e-02 -1.932 0.053511 .
## xbestCondition2PosN -9.288e-01 8.233e-02 -11.282 < 2e-16 ***
## xbestCondition2RRAe -4.751e-01 1.662e-01 -2.858 0.004327 **
## xbestBldgTypeTwnhs -5.001e-02 1.974e-02 -2.533 0.011412 *
## xbestHouseStyle1Story -1.750e-02 1.125e-02 -1.555 0.120267
## xbestHouseStyle2.5Fin -9.306e-02 5.011e-02 -1.857 0.063540 .
## xbestHouseStyle2.5Unf 6.948e-02 3.587e-02 1.937 0.052923 .
## xbestHouseStyle2Story -1.909e-02 1.309e-02 -1.459 0.144796
## xbestOverallQual 4.507e-02 4.075e-03 11.061 < 2e-16 ***
## xbestOverallCond 3.851e-02 3.582e-03 10.752 < 2e-16 ***
## xbestYearBuilt 2.042e-03 2.419e-04 8.439 < 2e-16 ***
## xbestYearRemodAdd 8.796e-04 2.262e-04 3.889 0.000105 ***
## xbestRoofStyleShed 3.562e-01 1.253e-01 2.844 0.004528 **
## xbestRoofMatlCompShg 2.774e+00 1.273e-01 21.798 < 2e-16 ***
## xbestRoofMatlMembran 3.171e+00 1.752e-01 18.105 < 2e-16 ***
## xbestRoofMatlMetal 3.038e+00 1.736e-01 17.499 < 2e-16 ***
## xbestRoofMatlRoll 2.786e+00 1.649e-01 16.897 < 2e-16 ***
## xbestRoofMatlTar&Grv 2.823e+00 1.316e-01 21.454 < 2e-16 ***
## xbestRoofMatlWdShake 2.750e+00 1.375e-01 20.007 < 2e-16 ***
## xbestRoofMatlWdShngl 2.832e+00 1.335e-01 21.210 < 2e-16 ***
## xbestExterior1stBrkComm -2.223e-01 8.083e-02 -2.750 0.006043 **
## xbestExterior1stBrkFace 5.533e-02 1.759e-02 3.146 0.001690 **
## xbestExterior1stCBlock -1.221e-01 1.063e-01 -1.149 0.250871
## xbestExterior1stCemntBd -9.214e-02 6.328e-02 -1.456 0.145572
## xbestExterior1stHdBoard -2.106e-02 9.233e-03 -2.281 0.022695 *
## xbestExterior1stMetalSd 3.414e-02 3.482e-02 0.981 0.327009
## xbestExterior1stWd Sdng -5.200e-02 1.737e-02 -2.994 0.002805 **
## xbestExterior2ndCBlock NA NA NA NA
## xbestExterior2ndCmentBd 1.078e-01 6.387e-02 1.688 0.091632 .
## xbestExterior2ndMetalSd -2.332e-02 3.491e-02 -0.668 0.504290
## xbestExterior2ndWd Sdng 4.314e-02 1.705e-02 2.531 0.011486 *
## xbestMasVnrTypeBrkFace 3.599e-02 2.902e-02 1.240 0.215138
## xbestMasVnrTypeNone 2.806e-02 2.868e-02 0.979 0.327997
## xbestMasVnrTypeStone 5.264e-02 3.073e-02 1.713 0.086947 .
## xbestExterCondFa -1.019e-01 5.860e-02 -1.739 0.082273 .
## xbestExterCondGd -8.444e-02 5.523e-02 -1.529 0.126521
## xbestExterCondTA -6.340e-02 5.480e-02 -1.157 0.247490
## xbestFoundationPConc 3.250e-02 9.392e-03 3.460 0.000557 ***
## xbestFoundationStone 1.050e-01 4.479e-02 2.345 0.019168 *
## xbestFoundationWood -1.488e-01 6.331e-02 -2.351 0.018863 *
## xbestBsmtCondPo 1.864e-01 8.724e-02 2.137 0.032813 *
## xbestBsmtExposureGd 3.626e-02 1.185e-02 3.060 0.002259 **
## xbestBsmtExposureNo -1.372e-02 7.164e-03 -1.916 0.055630 .
## xbestBsmtFinType2BLQ -4.045e-02 2.050e-02 -1.973 0.048716 *
## xbestBsmtFinType2Unf 1.684e-02 9.977e-03 1.688 0.091634 .
## xbestBsmtUnfSF -6.426e-05 1.026e-05 -6.263 5.07e-10 ***
## xbestTotalBsmtSF 1.430e-04 1.544e-05 9.264 < 2e-16 ***
## xbestHeatingGasA 1.503e-01 3.650e-02 4.117 4.08e-05 ***
## xbestHeatingGasW 2.172e-01 4.375e-02 4.963 7.81e-07 ***
## xbestHeatingWall 2.131e-01 6.604e-02 3.227 0.001282 **
## xbestHeatingQCGd -1.962e-02 8.609e-03 -2.279 0.022830 *
## xbestHeatingQCTA -3.092e-02 8.057e-03 -3.838 0.000130 ***
## xbestCentralAirY 6.336e-02 1.525e-02 4.154 3.47e-05 ***
## xbestX1stFlrSF 2.705e-04 1.766e-05 15.314 < 2e-16 ***
## xbestX2ndFlrSF 2.713e-04 1.755e-05 15.463 < 2e-16 ***
## xbestLowQualFinSF 2.957e-04 7.443e-05 3.972 7.49e-05 ***
## xbestGrLivArea NA NA NA NA
## xbestBsmtFullBath 2.886e-02 7.709e-03 3.743 0.000189 ***
## xbestHalfBath 1.465e-02 7.951e-03 1.843 0.065608 .
## xbestKitchenAbvGr -3.935e-02 1.639e-02 -2.400 0.016524 *
## xbestKitchenQualFa -6.725e-02 2.499e-02 -2.691 0.007210 **
## xbestKitchenQualGd -6.974e-02 1.363e-02 -5.116 3.56e-07 ***
## xbestKitchenQualTA -6.501e-02 1.574e-02 -4.130 3.85e-05 ***
## xbestFunctionalMaj2 -3.014e-01 5.277e-02 -5.712 1.37e-08 ***
## xbestFunctionalMod -9.172e-02 3.227e-02 -2.843 0.004541 **
## xbestFunctionalSev -3.083e-01 1.166e-01 -2.644 0.008285 **
## xbestFunctionalTyp 4.074e-02 1.350e-02 3.018 0.002589 **
## xbestFireplaces 2.228e-02 5.557e-03 4.010 6.40e-05 ***
## xbestGarageTypeAttchd 4.771e-02 1.703e-02 2.801 0.005168 **
## xbestGarageTypeBuiltIn 2.901e-02 2.168e-02 1.338 0.181093
## xbestGarageTypeDetchd 3.832e-02 1.709e-02 2.242 0.025093 *
## xbestGarageCars 1.939e-02 9.408e-03 2.061 0.039488 *
## xbestGarageArea 1.187e-04 3.048e-05 3.894 0.000103 ***
## xbestGarageQualFa -5.842e-02 2.303e-02 -2.536 0.011315 *
## xbestGarageQualTA -1.868e-02 1.808e-02 -1.034 0.301542
## xbestWoodDeckSF 1.003e-04 2.506e-05 4.003 6.59e-05 ***
## xbestEnclosedPorch 1.159e-04 5.240e-05 2.212 0.027141 *
## xbestX3SsnPorch 1.381e-04 9.669e-05 1.428 0.153542
## xbestScreenPorch 2.527e-04 5.262e-05 4.802 1.75e-06 ***
## xbestSaleTypeConLD 1.290e-01 3.728e-02 3.460 0.000558 ***
## xbestSaleTypeCWD 7.657e-02 5.373e-02 1.425 0.154357
## xbestSaleTypeNew 1.091e-01 1.521e-02 7.176 1.18e-12 ***
## xbestSaleConditionAdjLand 8.365e-02 5.605e-02 1.493 0.135800
## xbestSaleConditionNormal 5.456e-02 1.016e-02 5.370 9.25e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1035 on 1356 degrees of freedom
## Multiple R-squared: 0.9376, Adjusted R-squared: 0.9328
## F-statistic: 197.8 on 103 and 1356 DF, p-value: < 2.2e-16mse<-(sum((bestmodel$residuals)^2))/1460
mse## [1] 0.009951527各种方法对比
jieguo<-read.csv("jieguo.csv",header = T)
library(knitr)
knitr::kable(jieguo)| 锘縨ethod | MSE |
|---|---|
| BASE | 0.1716800 |
| stepwise | 0.1319700 |
| LASSO | 0.1317300 |
| random forest | 0.1418900 |
| gbdt | 0.1313700 |
| BeSS | 0.0099515 |
使用bess方法建立的模型最终的均方误差只有\(0.009951527\),效果很好,但是也许建模过程中对因子化处理有些问题。通过对比得出相对而言bess方法是最优的。