这里由于还没有搞清楚具体的实施方案所以后五次作业还未上传。

第一次作业

第一题

help(stem)

## starting httpd help server ... done

data5<-c(12, 12, 11, 10, 9, 10, 12)
stem(data5)

## 
##   The decimal point is at the |
## 
##    9 | 0
##   10 | 00
##   11 | 0
##   12 | 000

第二题

x <- ((0:10000)/10000)*2*pi
y <- x^3 + sin(x)*cos(x)
plot(x, y, col="blue", type="l", xlab="自变量X", ylab="函数Y", main="示意图")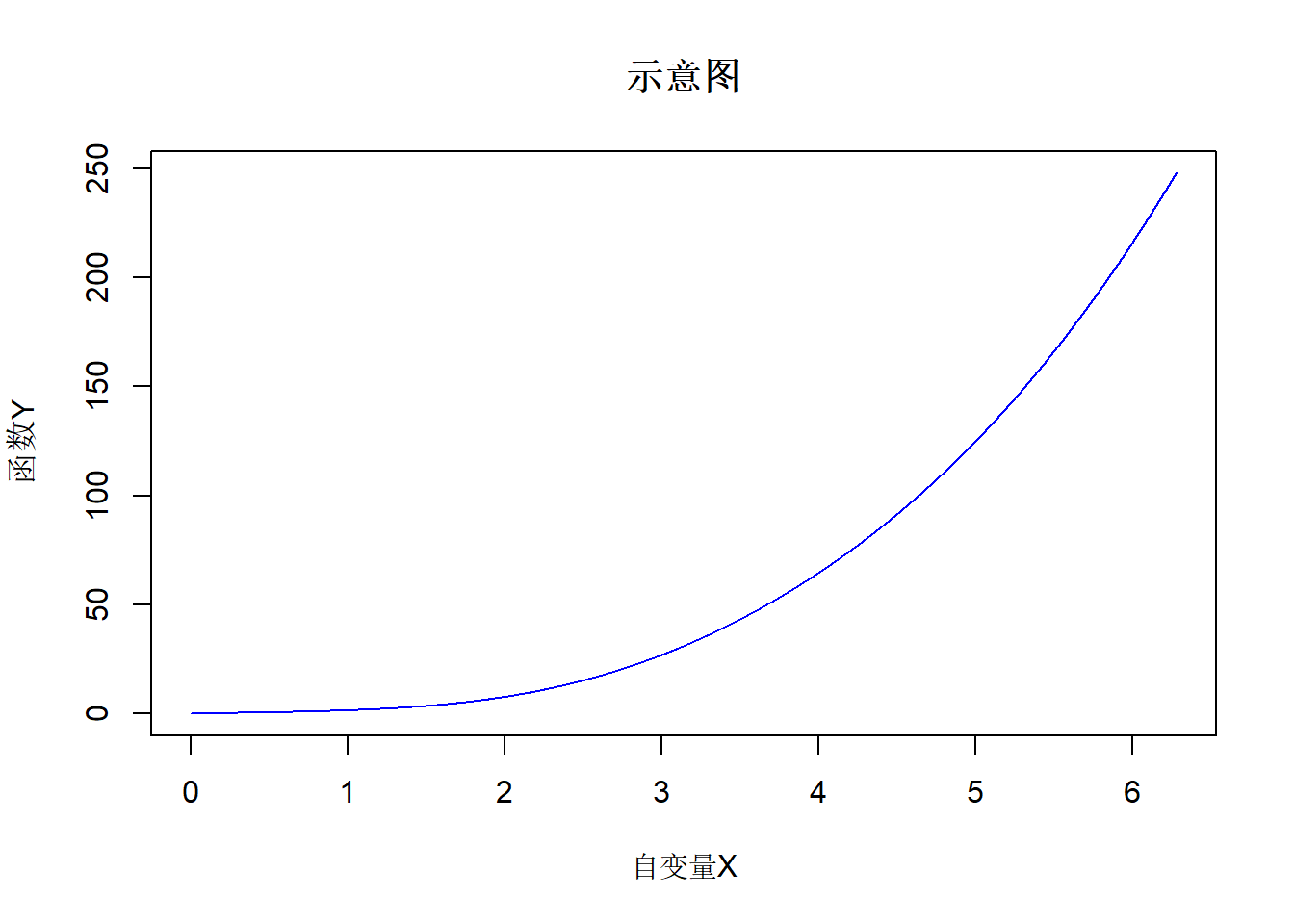

第二次作业

第一题

1.随机变量\(X~B(10,0.4)\),求分布律和分布函数，求\(P(X=3)\) 解：

x<-0:20
(y<-dbinom(x,10,0.4))#分布律

##  [1] 0.0060466176 0.0403107840 0.1209323520 0.2149908480 0.2508226560
##  [6] 0.2006581248 0.1114767360 0.0424673280 0.0106168320 0.0015728640
## [11] 0.0001048576 0.0000000000 0.0000000000 0.0000000000 0.0000000000
## [16] 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
## [21] 0.0000000000

(pbinom(x,10,0.4))#分布函数

##  [1] 0.006046618 0.046357402 0.167289754 0.382280602 0.633103258 0.833761382
##  [7] 0.945238118 0.987705446 0.998322278 0.999895142 1.000000000 1.000000000
## [13] 1.000000000 1.000000000 1.000000000 1.000000000 1.000000000 1.000000000
## [19] 1.000000000 1.000000000 1.000000000

求\(P(X=3)\)

(pbinom(3,10,0.4))

## [1] 0.3822806

第二题

随机变量\(X\)服从1到5的离散均匀分布，求\(P(1<X<3)\)

(punif(3,1,5)-punif(1,1,5))

## [1] 0.5

第三题

随机变量\(X~U(2,4)\),画出密度函数和分布函数，求\(P(2.5<X<3.5)\)

x<-seq(0,8,0.01)
y<-dunif(x,2,4)
z<-punif(x,2,4)
data1<-data.frame(a=x,b=y,c=z)
#g<-ggplot(data = data1,aes(x=a,y=b),col="red")+geom_line()
library(ggplot2)
ggplot()+geom_line(data=data1,aes(x=a,y=c),col="blue")+geom_line(data = data1,aes(x=a,y=b),col="red")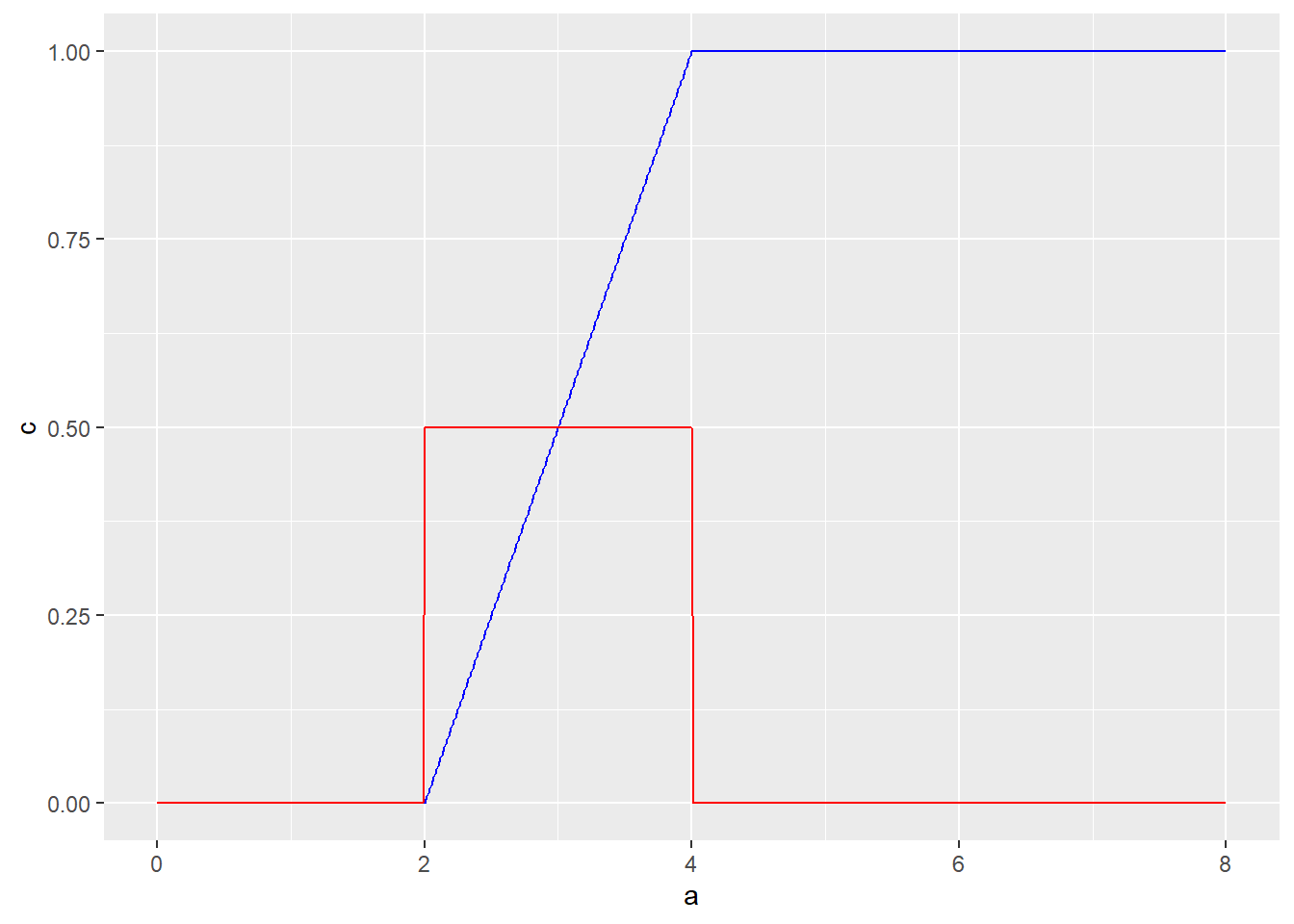

(punif(3.5,2,4)-punif(2.5,2,4))

## [1] 0.5

第四题

随机变量\(X~E(4)\)画出密度函数和分布函数，求\(P(1<X<5)\)

x<-seq(0,5,0.5)
y<-dexp(x,4)
z<-pexp(x,4)
plot(x,z,type = "l",col="blue")
lines(x,y,type ="l",col="red")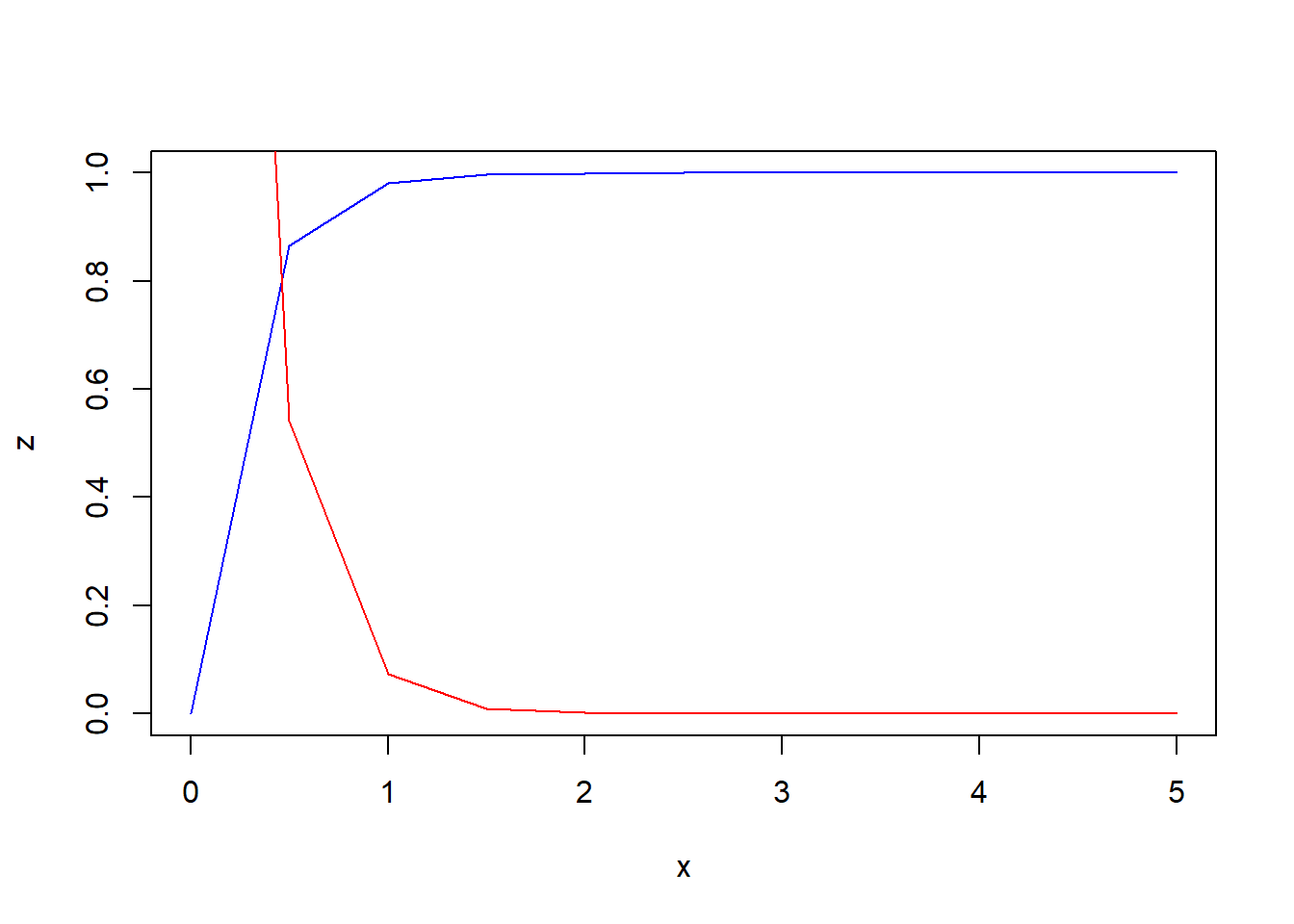

(pexp(5,4)-pexp(1,4))

## [1] 0.01831564

第五题

x<-seq(-5,5,0.01)
y<-dnorm(x,1,2)
z<-pnorm(x,1,2)
plot(x,y,type = "l",col="red")
lines(x,z,type="l",col="blue")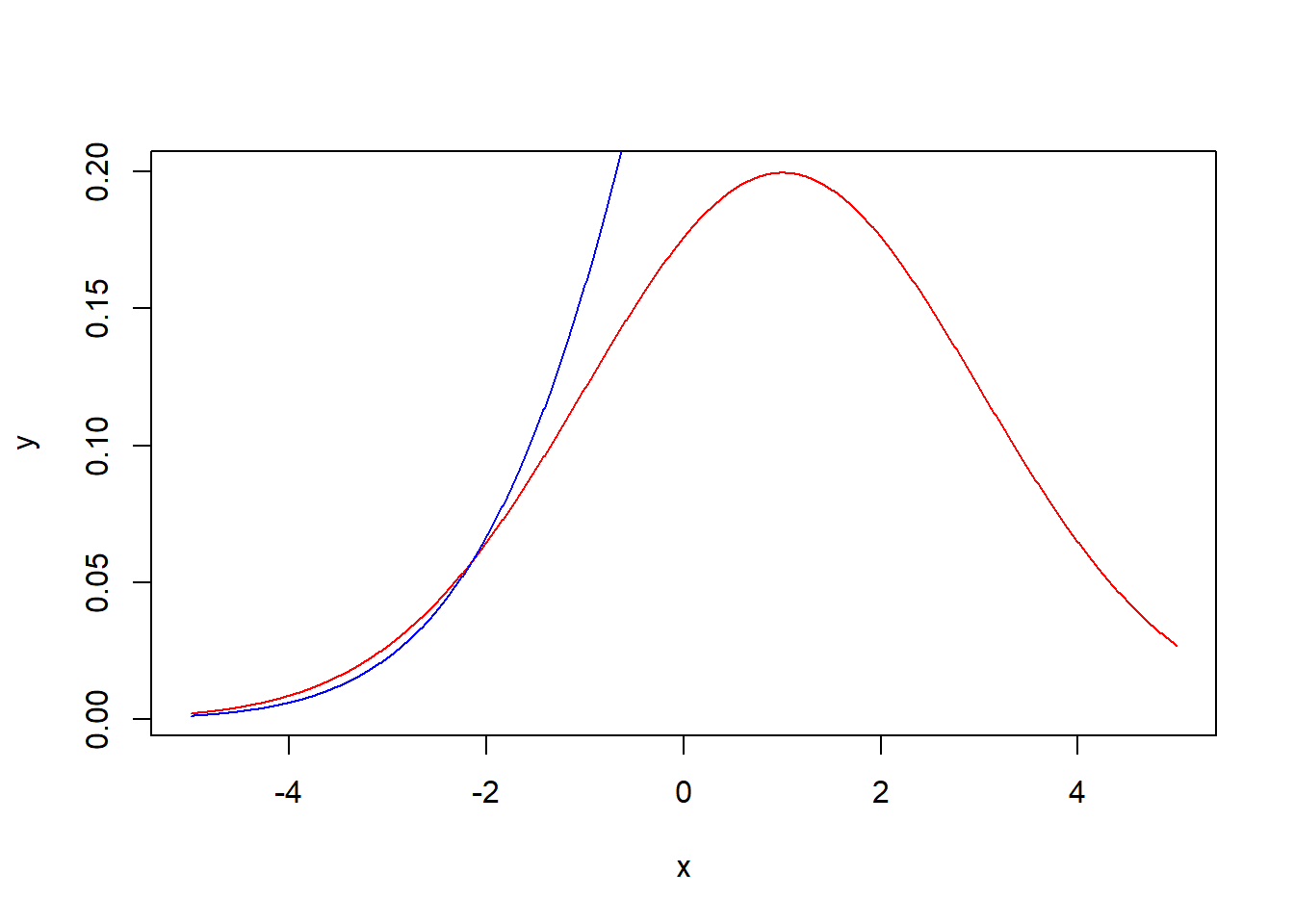

(pnorm(3,1,2)-pnorm(-2,1,2))

## [1] 0.7745375

第三次作业

第一题

#help(tapply)
data7<-data.frame(name = c("jack","rose","mike"),age = c(5,6,7),score = c(60,80,90))
aver<-tapply(data7$score,data7$age,mean)
aver

##  5  6  7 
## 60 80 90

第二题

data8<-read.table(file= "D:/rclasstongjiruanjian/user.txt",header = T)

table(data8[,2])

## 
##  F  M 
##  9 10

table(data8[,3])

## 
## 11 12 13 14 15 16 
##  2  5  3  4  4  1

d<-tapply(data8[,4],data8[,2],mean)
d

##        F        M 
## 60.58889 63.91000

e<-tapply(data8[,4],data8[,3],mean)
e

##       11       12       13       14       15       16 
## 54.40000 59.44000 61.43333 64.90000 65.62500 72.00000

list<-list(sexcount=table(data8[,2]),agecount = table(data8[,3]),sexheight = d,ageheight = e)
list

## $sexcount
## 
##  F  M 
##  9 10 
## 
## $agecount
## 
## 11 12 13 14 15 16 
##  2  5  3  4  4  1 
## 
## $sexheight
##        F        M 
## 60.58889 63.91000 
## 
## $ageheight
##       11       12       13       14       15       16 
## 54.40000 59.44000 61.43333 64.90000 65.62500 72.00000

第三题

q<-rnorm(100,0,1)
juzhen<-matrix(q,5,20)
juzhen

##            [,1]        [,2]       [,3]       [,4]        [,5]       [,6]
## [1,]  1.5986562  0.30706179 -0.1007051  0.8483531  0.06638324 -0.5298676
## [2,] -0.3581486  1.97126697  0.4216181  1.4305401 -1.52644143 -2.2966440
## [3,] -1.5189005 -0.23914437 -0.5018847  0.3364413  1.43585825  0.1200956
## [4,]  2.5078224 -0.04351416 -0.2460952 -0.7944763  0.50331543 -0.4103107
## [5,] -1.2820549 -1.91739324 -1.7046170 -1.7517257  0.62260580 -0.5075274
##             [,7]       [,8]        [,9]      [,10]      [,11]      [,12]
## [1,] -0.74443046  0.9086036 -0.37306092  1.7876926  0.9790418  0.7291389
## [2,]  0.33059016 -0.5551763  0.88875684  0.8272038  1.2917029 -0.7235849
## [3,] -1.42660959  2.4850482  0.11616118  0.8672004 -0.0896518  0.1030129
## [4,]  0.08865374  0.7419789  2.53191605  0.1761840 -0.5018744 -0.1971965
## [5,]  0.94713663  0.6526863 -0.08804171 -0.6228922  2.0188305  0.5249277
##           [,13]       [,14]       [,15]      [,16]      [,17]      [,18]
## [1,] -1.2371429  1.09028585 -1.34780318 -1.1959029 -0.6514890  0.7002292
## [2,] -1.7600375  0.02826079 -0.04768925  0.7244111  0.2583115  0.9247852
## [3,]  0.9720902 -1.40024185 -1.25591583 -0.7060724  0.2741938 -0.6491607
## [4,]  0.1911341  0.50819406 -0.88966257 -1.4753059 -1.4796076  0.2709893
## [5,]  0.0694099  0.46707881 -0.16562858 -0.4809066  0.7544185 -1.5929476
##           [,19]      [,20]
## [1,] -0.4807801 -1.7424240
## [2,] -0.8642800  0.6011741
## [3,]  0.4939659 -1.1315631
## [4,] -0.8525664  1.8595967
## [5,]  1.3993939 -0.8192179

write.table(as.vector(juzhen),file="juzhen.txt")
w<-read.table("juzhen.txt")
y<-matrix(t(w),5,20)

第四题

t<-0
for( i in 1:100)
    t<-(t+1/i)
    print(t)

## [1] 5.187378

第四次作业

课后第一题

findmax <- function(x){
  p<-which(x==x[which.max(x)],arr.ind = T)
  list(maxvalue = x[p],location=which(x==x[which.max(x)],arr.ind = T))
}
A = matrix(floor(rnorm(100,0,4)),4,25)
findmax(A)

## $maxvalue
## [1] 8 8 8
## 
## $location
##      row col
## [1,]   4   7
## [2,]   1   9
## [3,]   2  19

作业第二题

test<-function(x,y){
  p<-(x^2+sin(x*y)+2*y)
  return(p)
}

第三节课第三题

fillna<-function(a){
  m<-which(is.na(a),arr.ind = T)
  a[m]<-c(rep(mean(a,na.rm =TRUE),nrow(m)))
  return(a)
  
}
A=matrix(floor(rnorm(100,0,4)),4,25)
A[2,5]=NA; A[4,8]=NA; A[3,15]=NA
fillna(A)

##      [,1] [,2] [,3] [,4]        [,5] [,6] [,7]        [,8] [,9] [,10] [,11]
## [1,]    4    2    5   -6  4.00000000   -2   -1  0.00000000    3     8    -2
## [2,]   -4    0    3   -3  0.01030928    3    3 -6.00000000   -9    -2    -4
## [3,]   -3    3    6   -1  0.00000000    6   -3 -2.00000000    3     1     5
## [4,]   -1   -3    1   -2 -6.00000000   -2   -6  0.01030928    9    -3     5
##      [,12] [,13] [,14]       [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22]
## [1,]    -4    -6    -5 -1.00000000     1     3    -4     2    -6     9     6
## [2,]    -5     2     5 -3.00000000    -3     5    -1     3    -2     3    -1
## [3,]     6     1     0  0.01030928    -4     1   -14     4     1     3    -3
## [4,]    -1     5    -6  0.00000000    -4     6    -3     1    -3     0    -3
##      [,23] [,24] [,25]
## [1,]     5     4    -2
## [2,]    -1    -5     4
## [3,]     3    -1     0
## [4,]     1     1     4

第三节课第四题

fzero<-function(f, a, b, eps=1e-5){
  if   (f(a)*f(b)>0)
    list (fail="finding root is fail!")
  else {repeat { 
    if (abs(b-a)<eps)   break
    x<-(a+b)/2
    if  (f(a)*f(b)<0)  b<-x else a<-x
  }
    list(root=(a+b)/2, fun=f(x))
  }
}
f<-function(x) {x^3-x-1}  
fzero(f,1,2,1e-5)

## $root
## [1] 1.249996
## 
## $fun
## [1] -0.2969031

第五次作业

data <- read.table("cl.txt", header=TRUE)
names(data) <- c("name", "age", "height", "weight", "sex")
plot(data$height, data$weight, main="Regression on Height and Weight",
     xlab="Height", ylab="Weight")

par(mfrow=c(2, 2))
qqnorm(data$weight)
hist(data$weight)
boxplot(data$weight) 
qqplot(data$height, data$weight, main="QQPLOT", xlab="Height", ylab="Weight")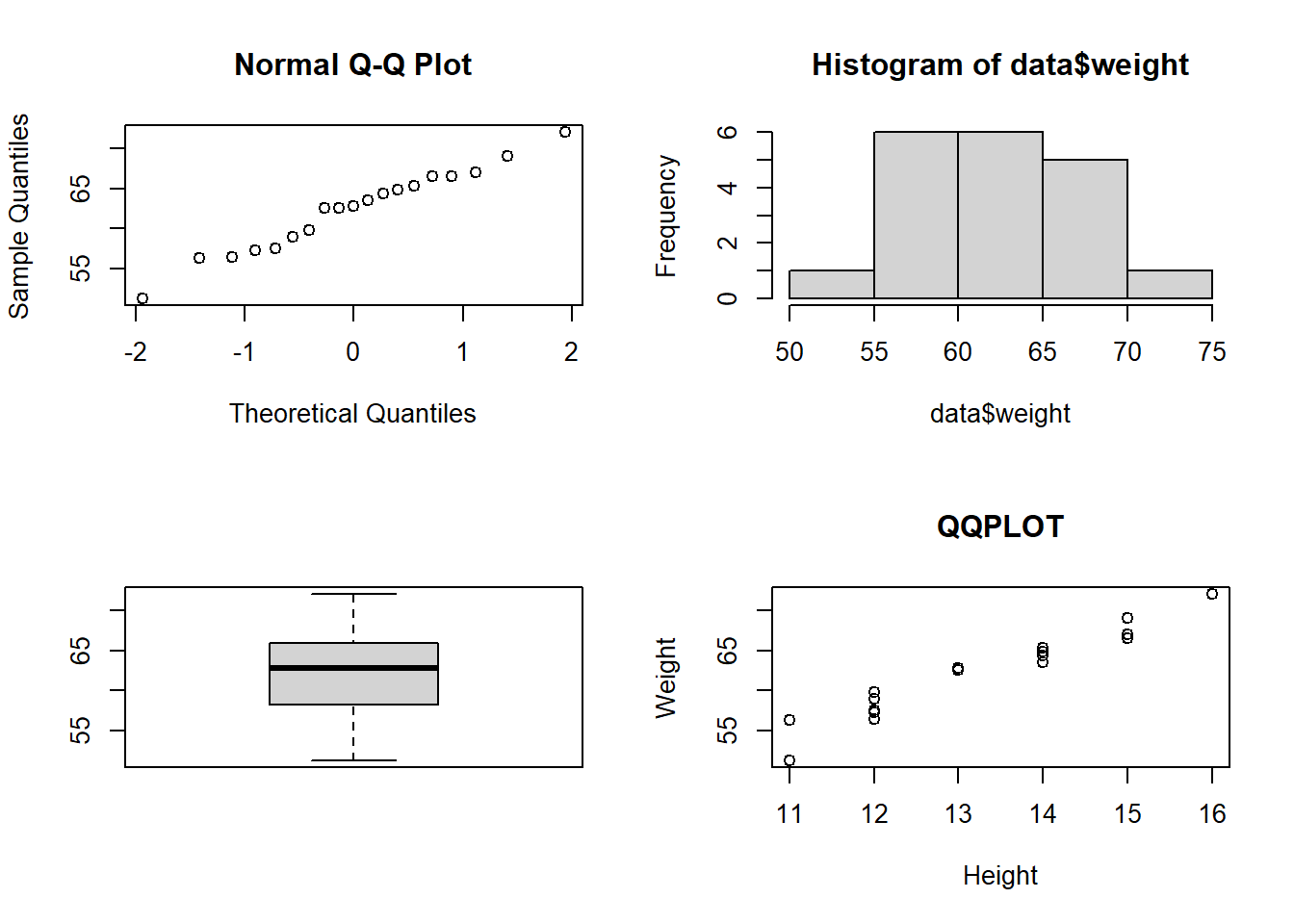

第二题

data <- read.table("cl.txt", header=TRUE)
plot(data)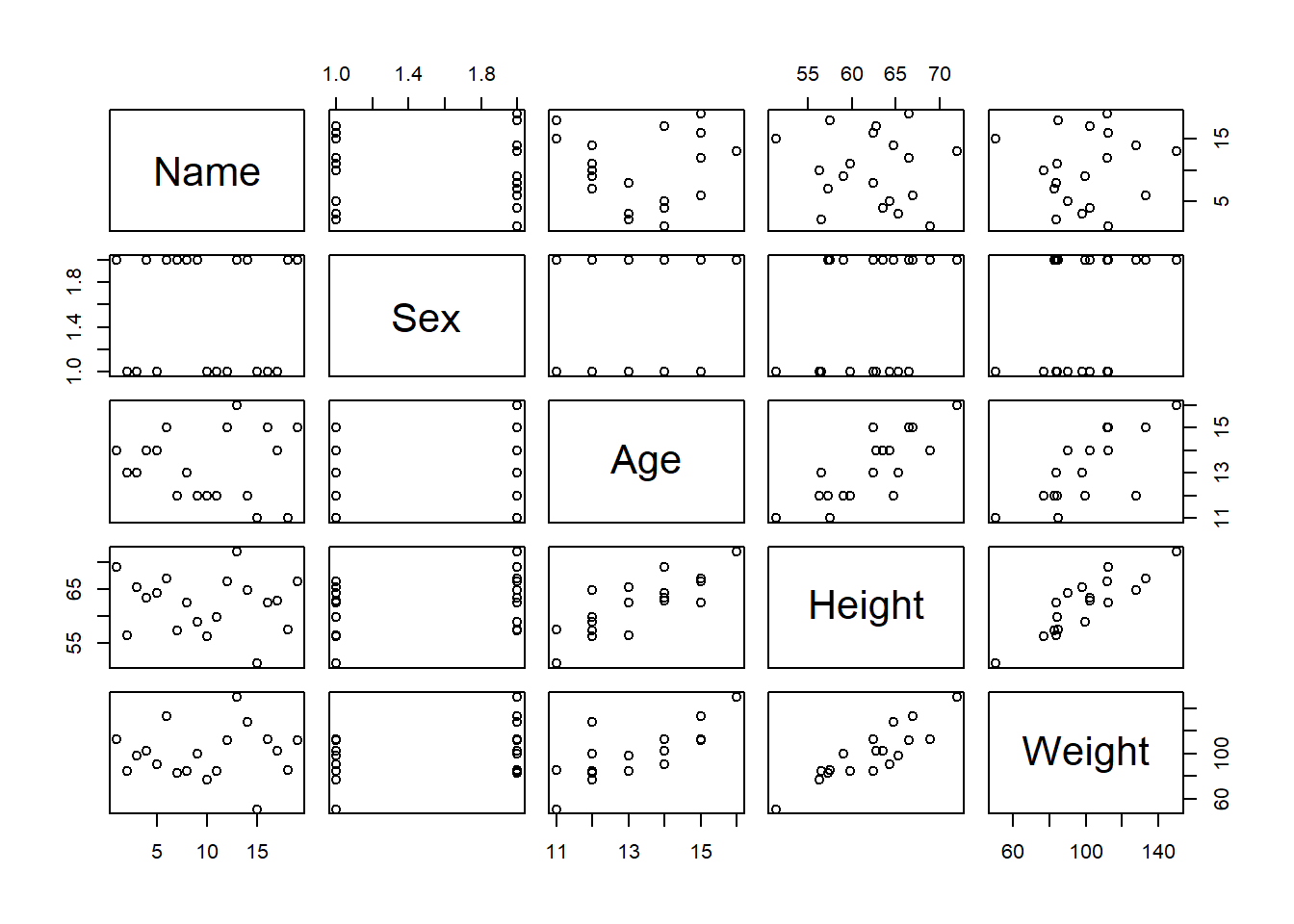

#coplot(data$Weight~data$Height|data$sex)
pairs(data[,c("Age", "Weight", "Height")])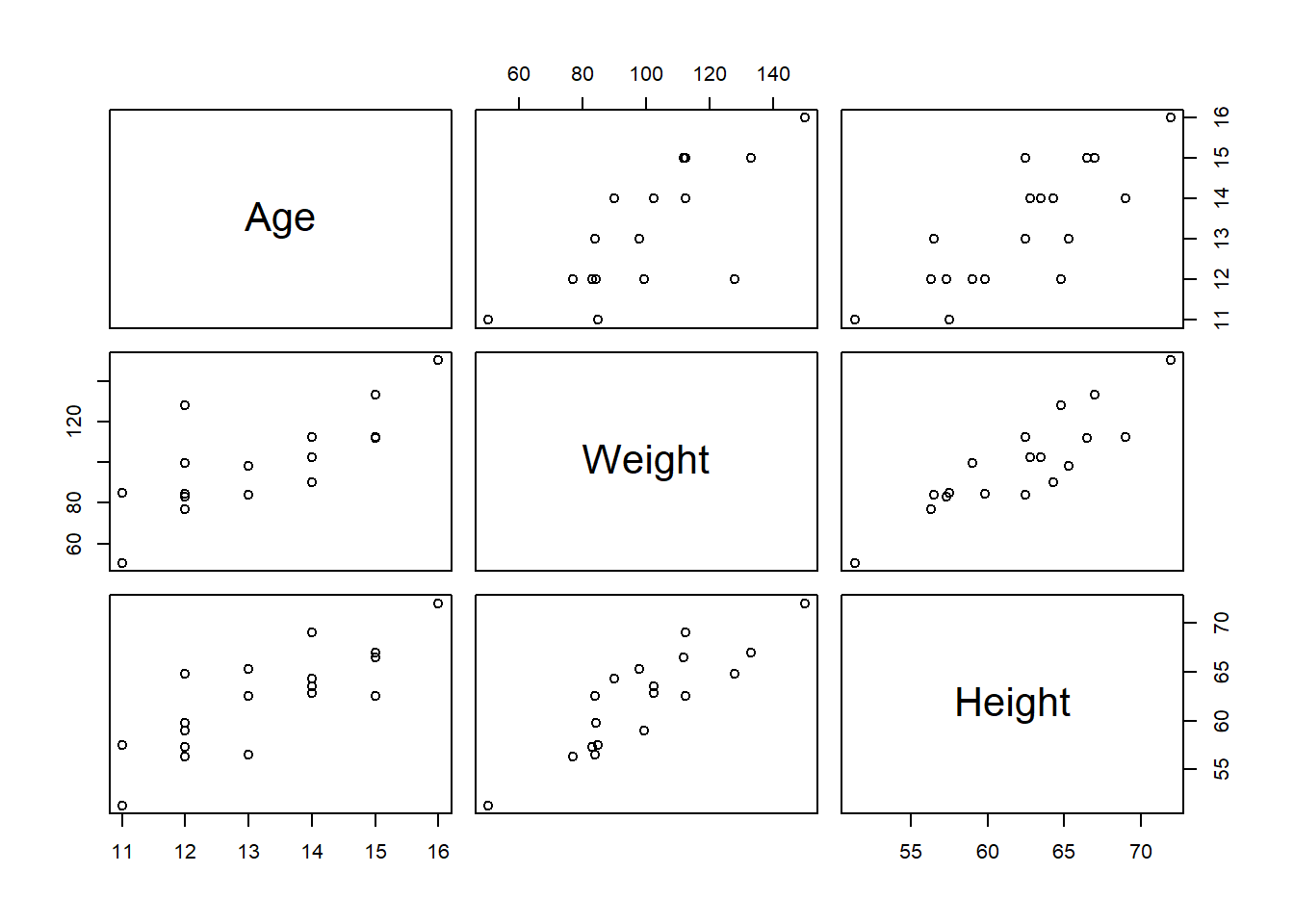

x <- data.frame(x1=rnorm(72, 0, 1),
             x2=rnorm(72, 0, 1),
             x3=rnorm(72, 0, 1),
             x4=rnorm(72, 0, 1)) 
t <- ts(x, start=c(2015, 1), frequency=12)
plot(t)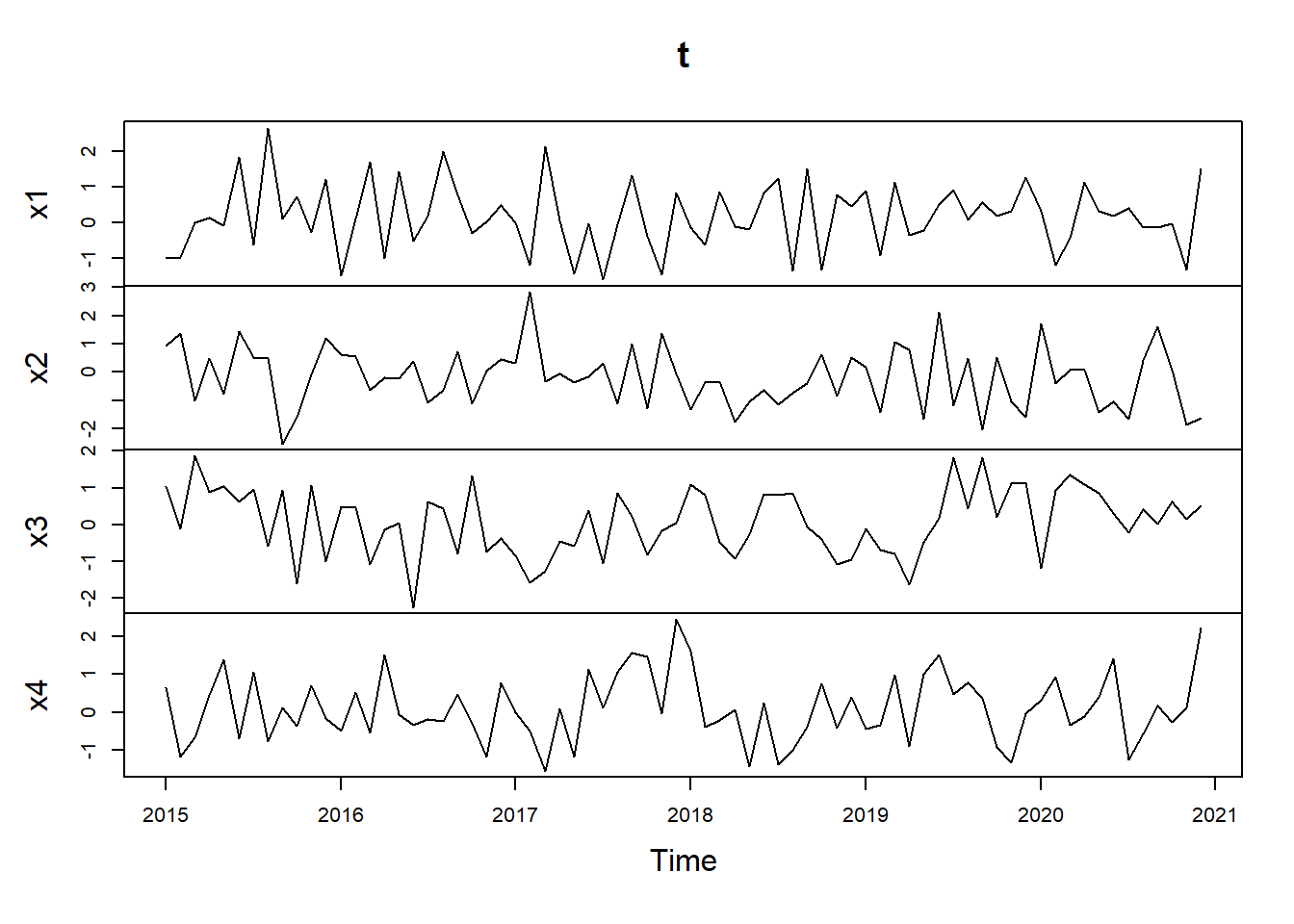

plot(x[,"x1"], x[,"x2"], col="black", xlab="x", ylab="y", main="normal values")
points(x[,"x3"], x[,"x4"], col="red")
legend(0, 0, "scatters", fill="blue")

plot(x[,"x1"], x[,"x2"], col="black", xlab="x", ylab="y", main="normal values")
lines(sort(x[,"x3"], decreasing=T), sort(x[,"x4"], decreasing=T), col="blue",type="o")
text(0, 0, labels="* the position of (0,0)")

l <- lm(sort(x[,"x3"], decreasing=T)~sort(x[,"x4"], decreasing=T))
abline(l$coefficients)
abline(h=0,col="red")
abline(v=0,col="green")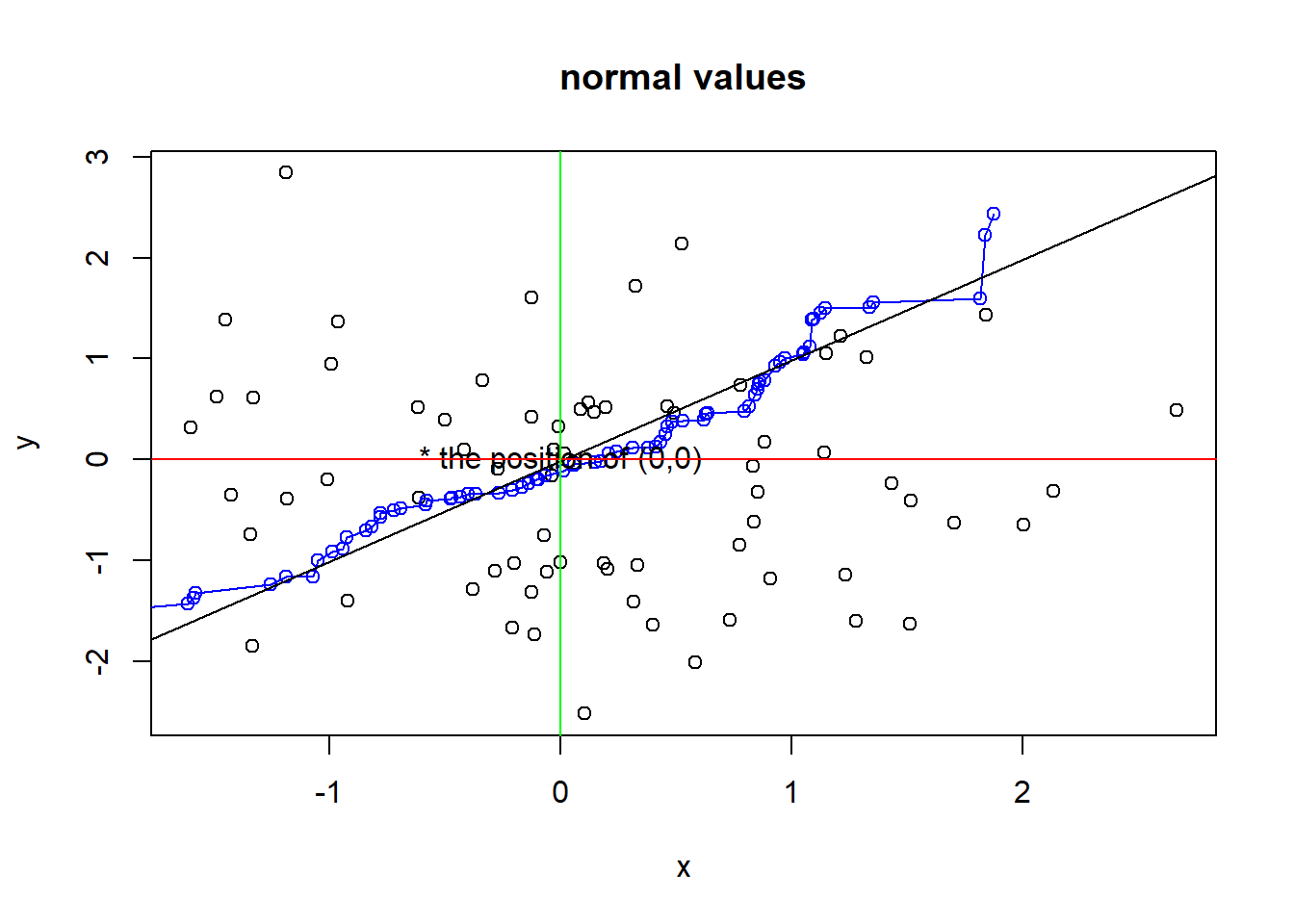

第三题

将屏幕分为四块并分别画出

y=sin(x)
z=3*cos(x)
a=sin(x)*cos(x)
b=sin(x)/x
par(mfrow=c(2,2))
x <- ((0:1000)/1000)*4*pi
plot(x, sin(x), col="red")
plot(x, 3*cos(x), col="blue")
plot(x, sin(x)*cos(x), col="yellow")
plot(x, sin(x)/x, col="green")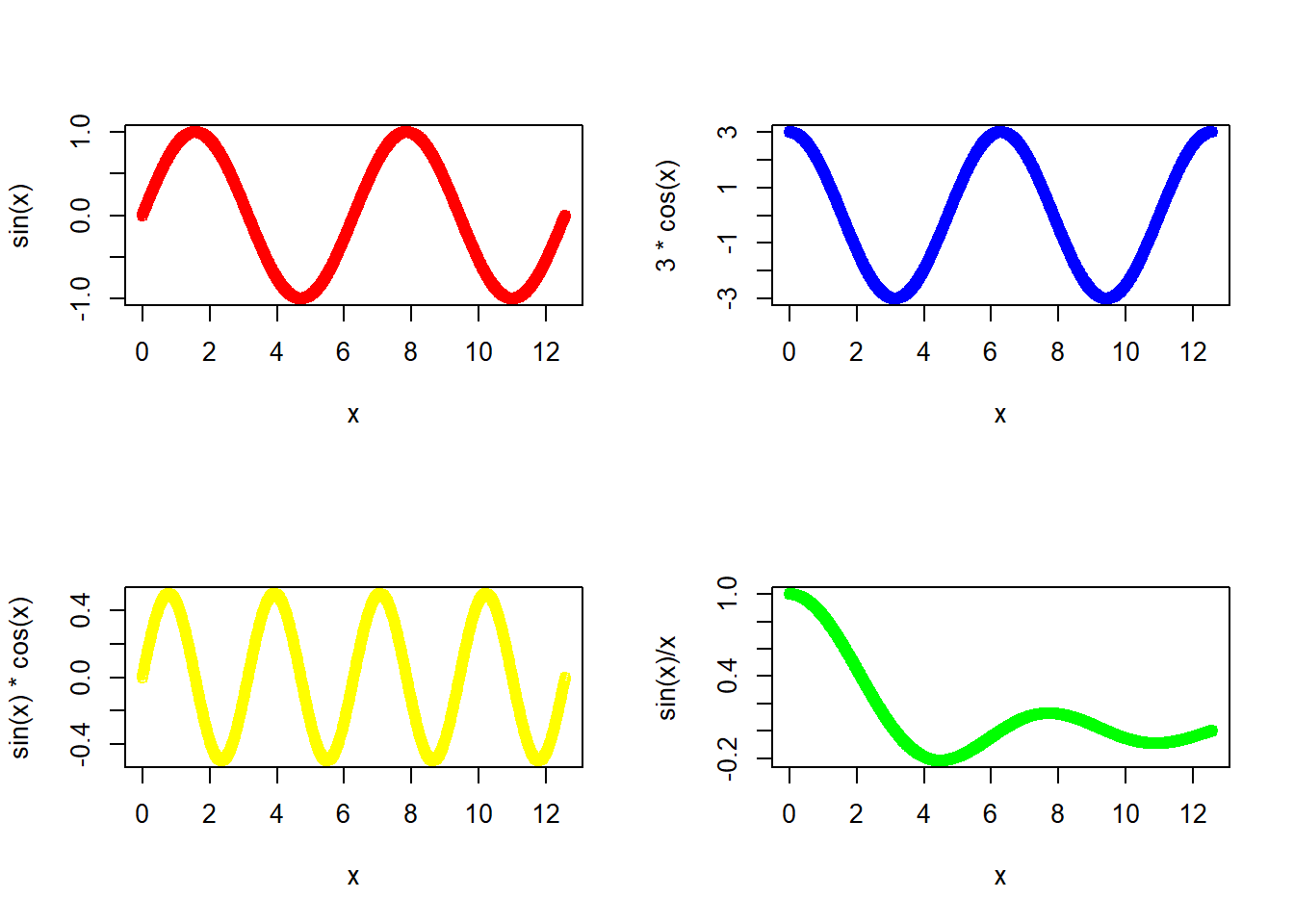

第六次作业

公司雇员数据分析

本次作业搜集到了公司的雇员数据，通过对数据进行统计分析，通过探索性分析得到相关结果。

数据展示

首先对读入的数据进行大致分析。

library(tidyverse)

## -- Attaching packages --------------------------------------- tidyverse 1.3.1 --

## v tibble  3.1.2     v dplyr   1.0.6
## v tidyr   1.1.3     v stringr 1.4.0
## v readr   1.4.0     v forcats 0.5.1
## v purrr   0.3.4

## -- Conflicts ------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

data<-read.csv("Employee.csv",header = T)
rmarkdown::paged_table(data)

从上表我们可以看出，该数据共有9个变量，其中分类变量有性别（男性或者女性），是否是少数人种（是或者否），连续型变量有工资薪水，起始工资等，变量种类挺多需要进一步分析。

可视化分析探索

首先进行因子化处理。

data$gender<-as.factor(data$gender)
data$minority<-as.factor(data$minority)
data$educ<-as.factor(data$educ)
data$jobcat<-as.factor(data$jobcat)

收入与性别分类箱线图

ggplot(data = data,aes(x=gender,y=salary))+geom_jitter(alpha=.35,color='#4169E1',size=2.2)+geom_boxplot(alpha=.7,color='#000080')+stat_summary(fun.y="mean",geom="point",color="#000080",shape=6,size=3.5)+theme(axis.title.y=element_text(size=15))+theme(axis.title.x=element_text(size=15))+theme(axis.text.y=element_text(size=15))+theme(axis.text.x=element_text(size=15))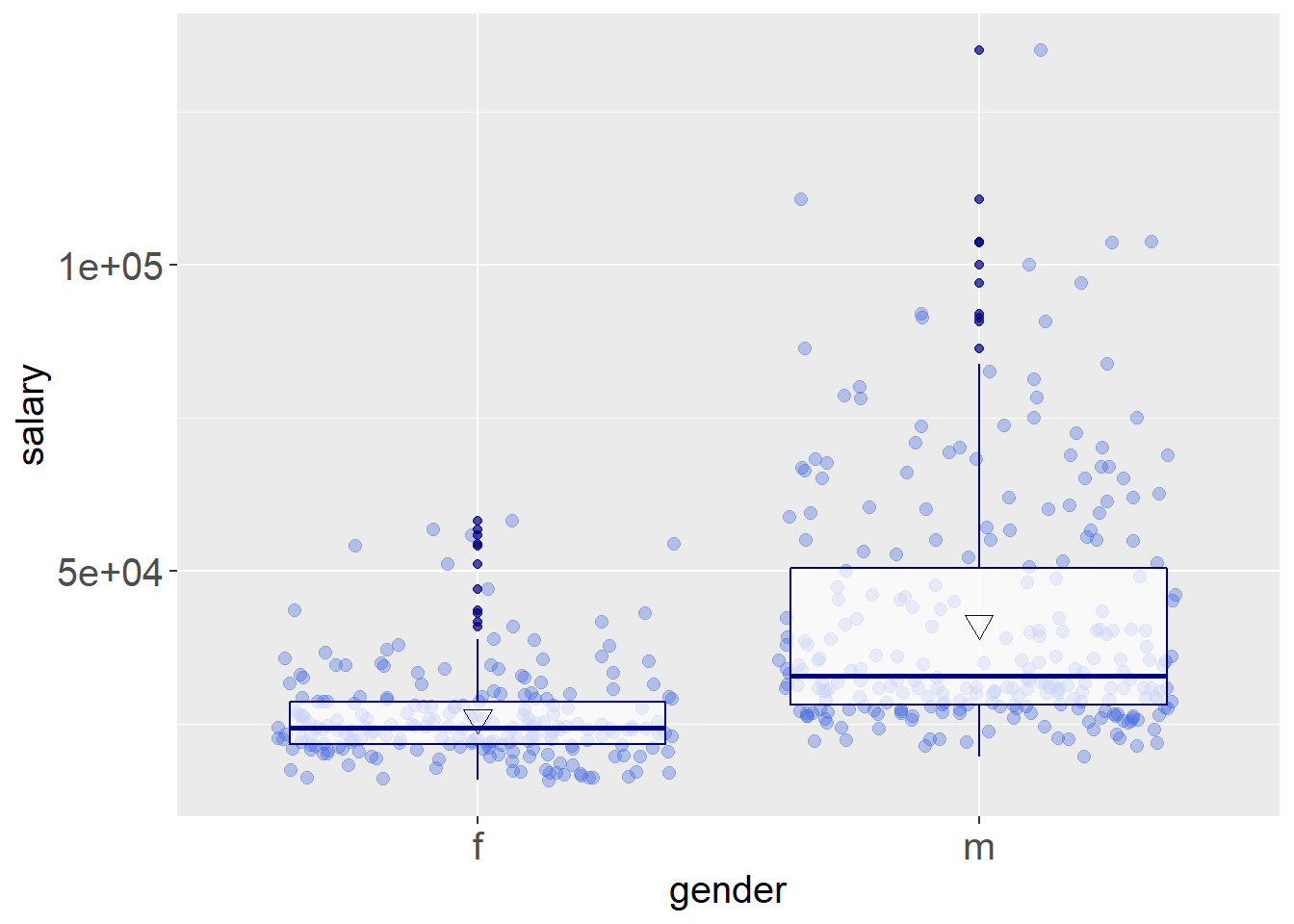

从收入与性别分类箱线图可以看出，男性的收入整体显著比女性高。女性收入较为集中，男性收入的分散程度大于女性。

收入与是否少数族裔箱线图

ggplot(data = data,aes(x=minority,y=salary))+geom_jitter(alpha=.35,color='#4169E1',size=2.2)+geom_boxplot(alpha=.7,color='#000080')+stat_summary(fun.y="mean",geom="point",color="#000080",shape=6,size=3.5)+theme(axis.title.y=element_text(size=15))+theme(axis.title.x=element_text(size=15))+theme(axis.text.y=element_text(size=15))+theme(axis.text.x=element_text(size=15))

## Warning: `fun.y` is deprecated. Use `fun` instead.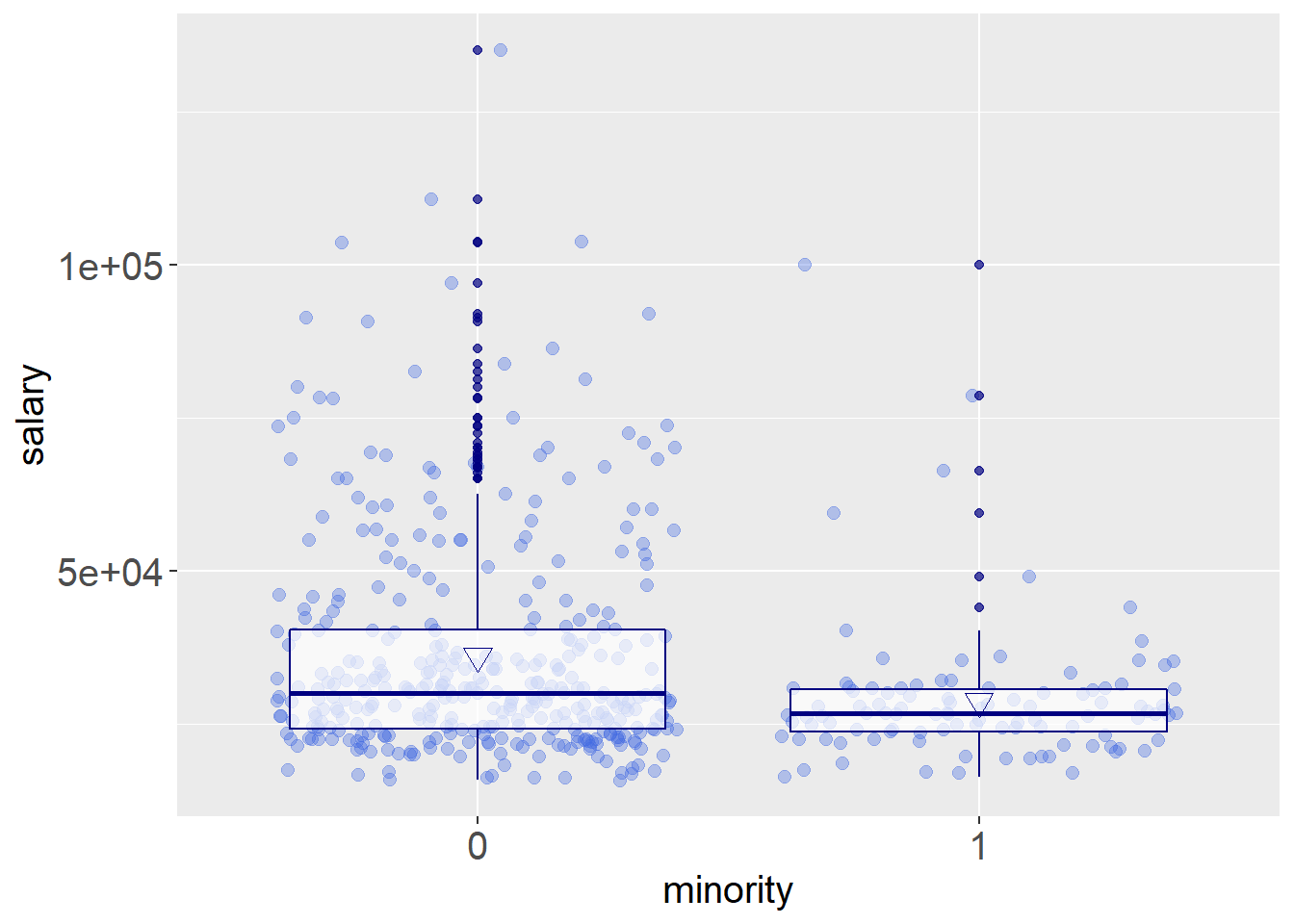

从收入与是否少数族裔图看出，非少数族裔的收入中位数与少数族裔的中位数的显著差别不大，但是非少数族裔的收入整体还是明显大于少数族裔的收入，说明在美国，少数族裔的收入是明显低于非少数族裔的。

收入与教育年限分类箱线图

ggplot(data = data,aes(x=educ,y=salary))+geom_jitter(alpha=.35,color='#4169E1',size=2.2)+geom_boxplot(alpha=.7,color='#000080')+stat_summary(fun.y="mean",geom="point",color="#000080",shape=6,size=3.5)+theme(axis.title.y=element_text(size=15))+theme(axis.title.x=element_text(size=15))+theme(axis.text.y=element_text(size=15))+theme(axis.text.x=element_text(size=15))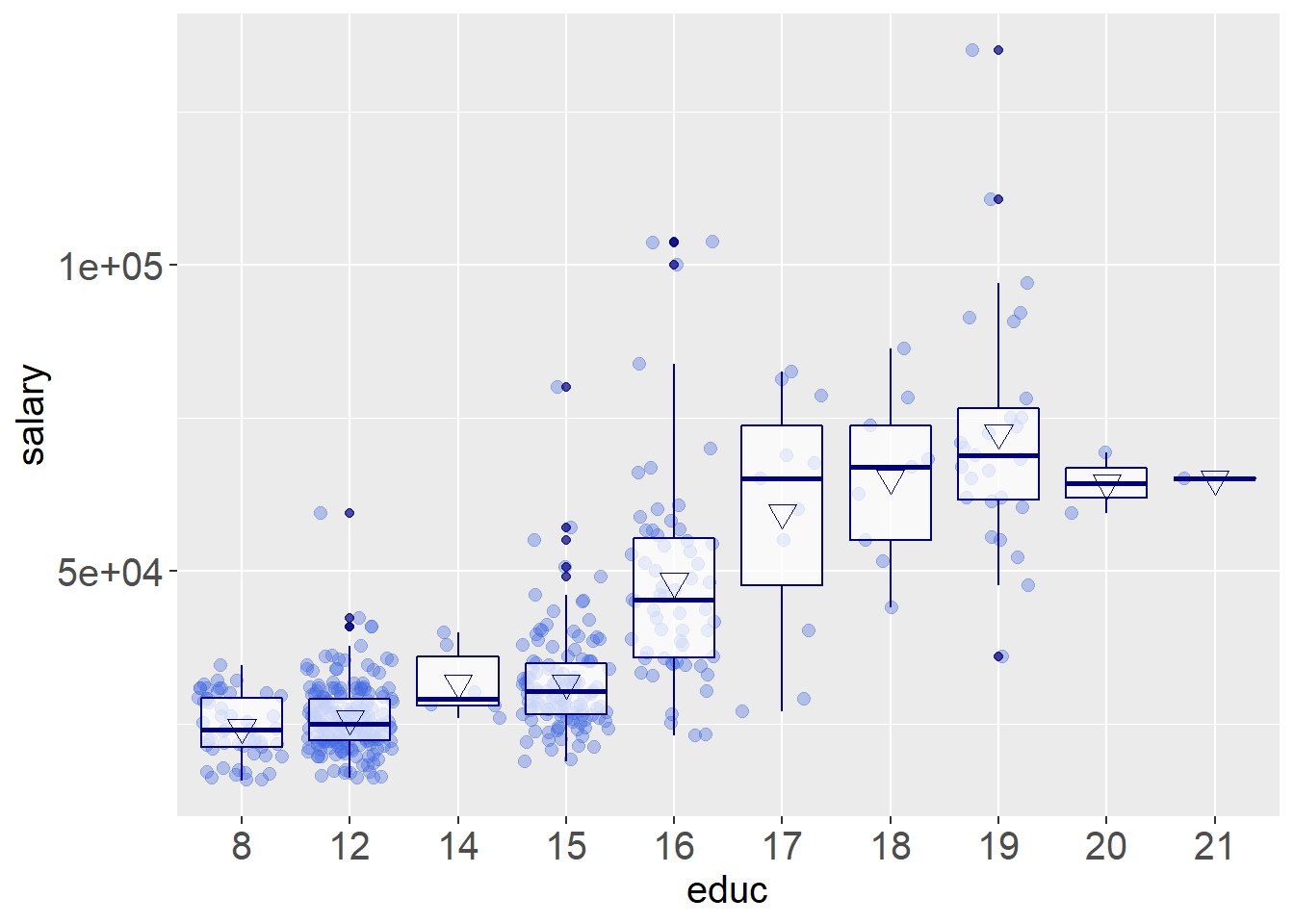

通过上图可以看出，受教育年限是明显的与收入大小成正比关系。在8和12这两个阶段相差不大，但是在16和17这两个阶段相差很大，一旦受教育程度从16提升到17，其收入程度会有很大的提升。并且随着年度的增加，这种边际效益会慢慢递减。

收入与职位等级分类箱线图

ggplot(data = data,aes(x=jobcat,y=salary))+geom_jitter(alpha=.35,color='#4169E1',size=2.2)+geom_boxplot(alpha=.7,color='#000080')+stat_summary(fun.y="mean",geom="point",color="#000080",shape=6,size=3.5)+theme(axis.title.y=element_text(size=15))+theme(axis.title.x=element_text(size=15))+theme(axis.text.y=element_text(size=15))+theme(axis.text.x=element_text(size=15))

## Warning: `fun.y` is deprecated. Use `fun` instead.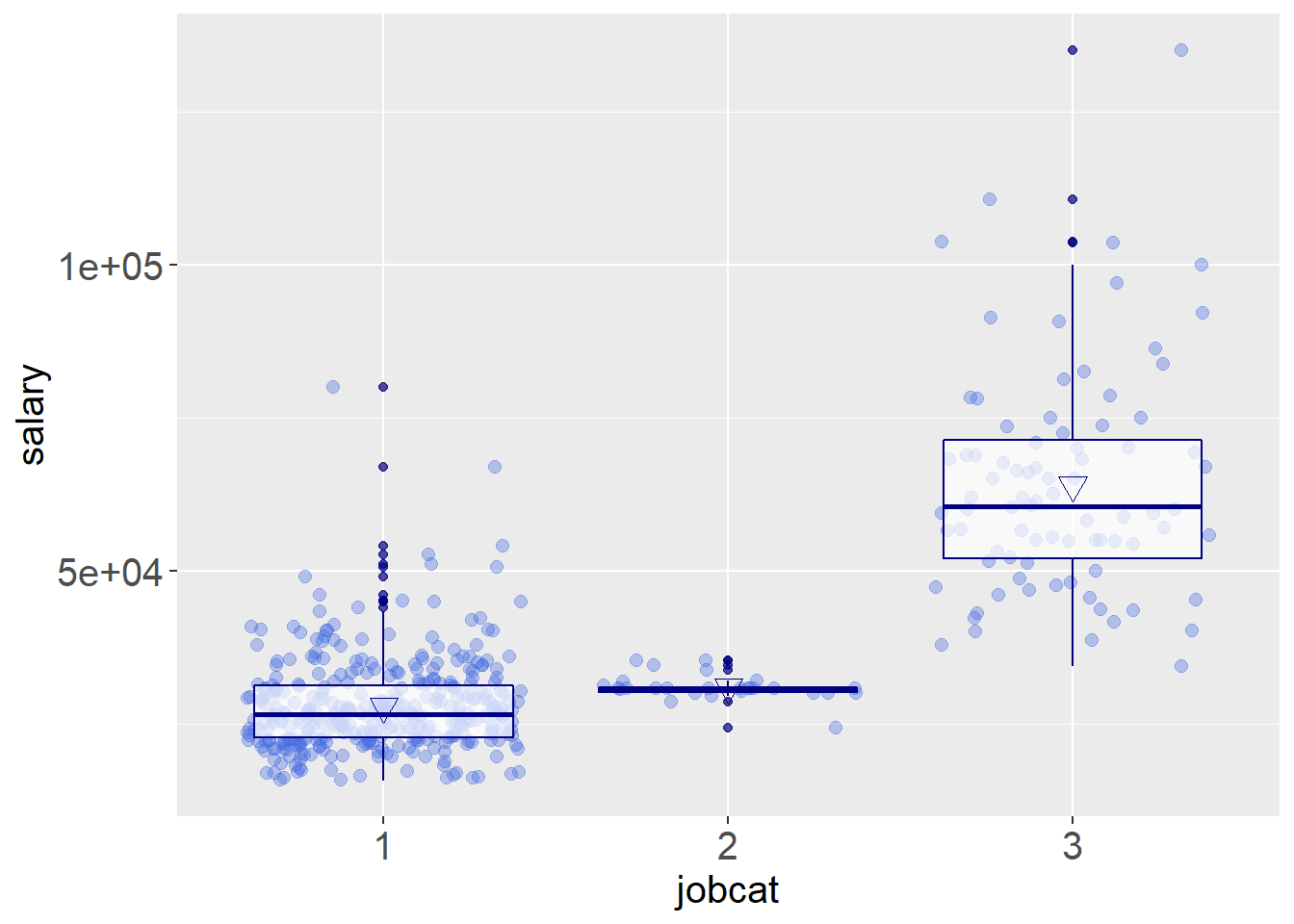

通过上图看出，职位等级的不同会明显提升收入水平，而在第二等级的数据十分紧密，初步推测是由于样本太小导致的，对数据中的jobcat进行计数分析如下。

knitr::kable(data%>%count(jobcat))

jobcat	n
1	363
2	27
3	84

从上图看出，位于第二等级的样本明显小于其他两个等级，所以导致箱线图过于紧密。

受教育年限与性别关系

data2<-read.csv("Employee.csv",header = T)#读取没有因子化的数据
ggplot(data2,aes(x=educ,fill=gender))+geom_histogram(position = "identity",alpha=0.6,bins = 25)+theme(axis.title.y=element_text(size=15))+theme(axis.title.x=element_text(size=15))+theme(axis.text.y=element_text(size=15))+theme(axis.text.x=element_text(size=15))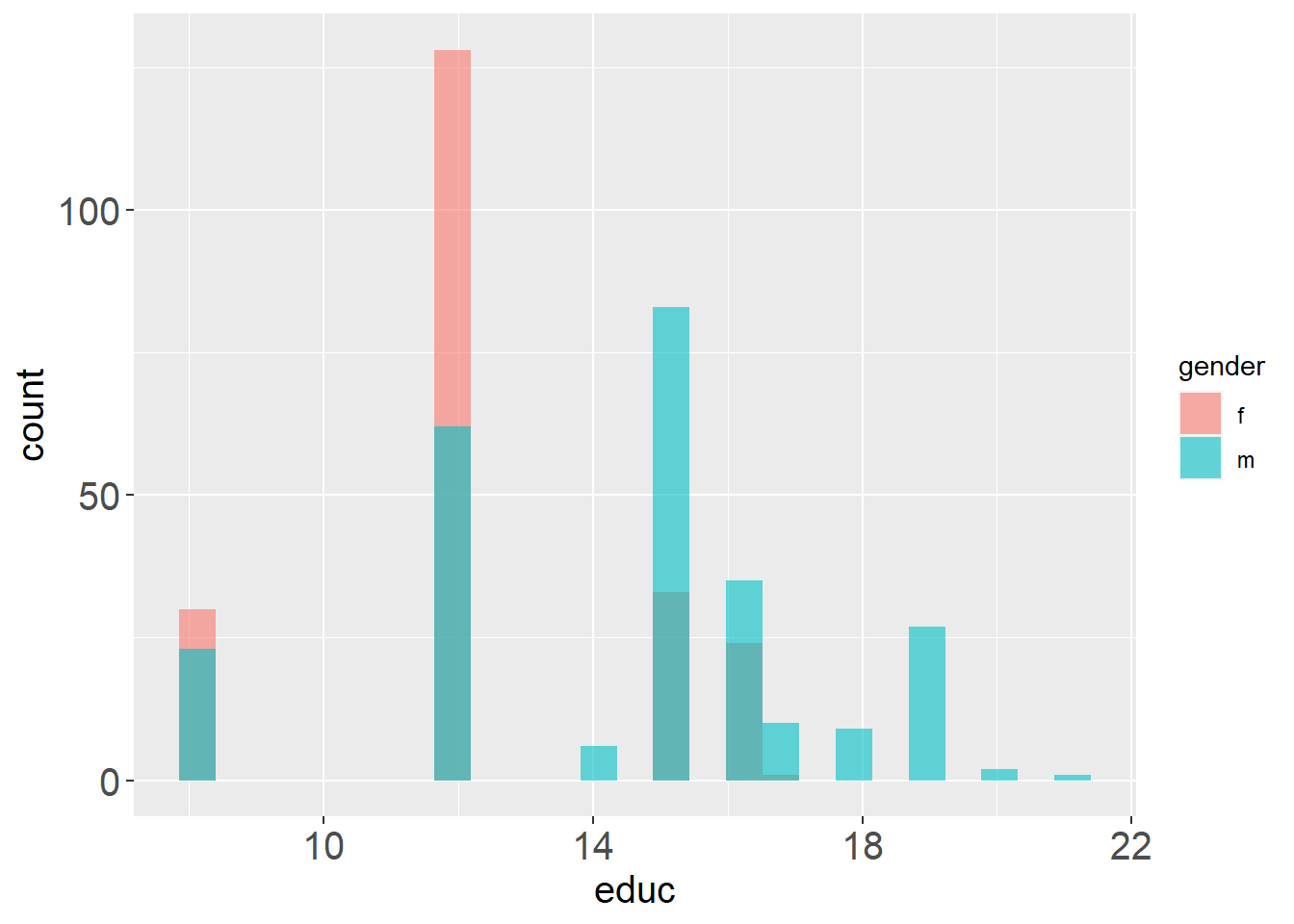

从上图看出，在搜集到的数据中，男性的受教育程度明显的多于女性，这也与受教育程度越高收入越高的事实相对应。

工作时间与性别关系图

ggplot(data2,aes(x=jobtime,fill=gender))+geom_histogram(position = "identity",alpha=0.6,bins = 25)+theme(axis.title.y=element_text(size=15))+theme(axis.title.x=element_text(size=15))+theme(axis.text.y=element_text(size=15))+theme(axis.text.x=element_text(size=15))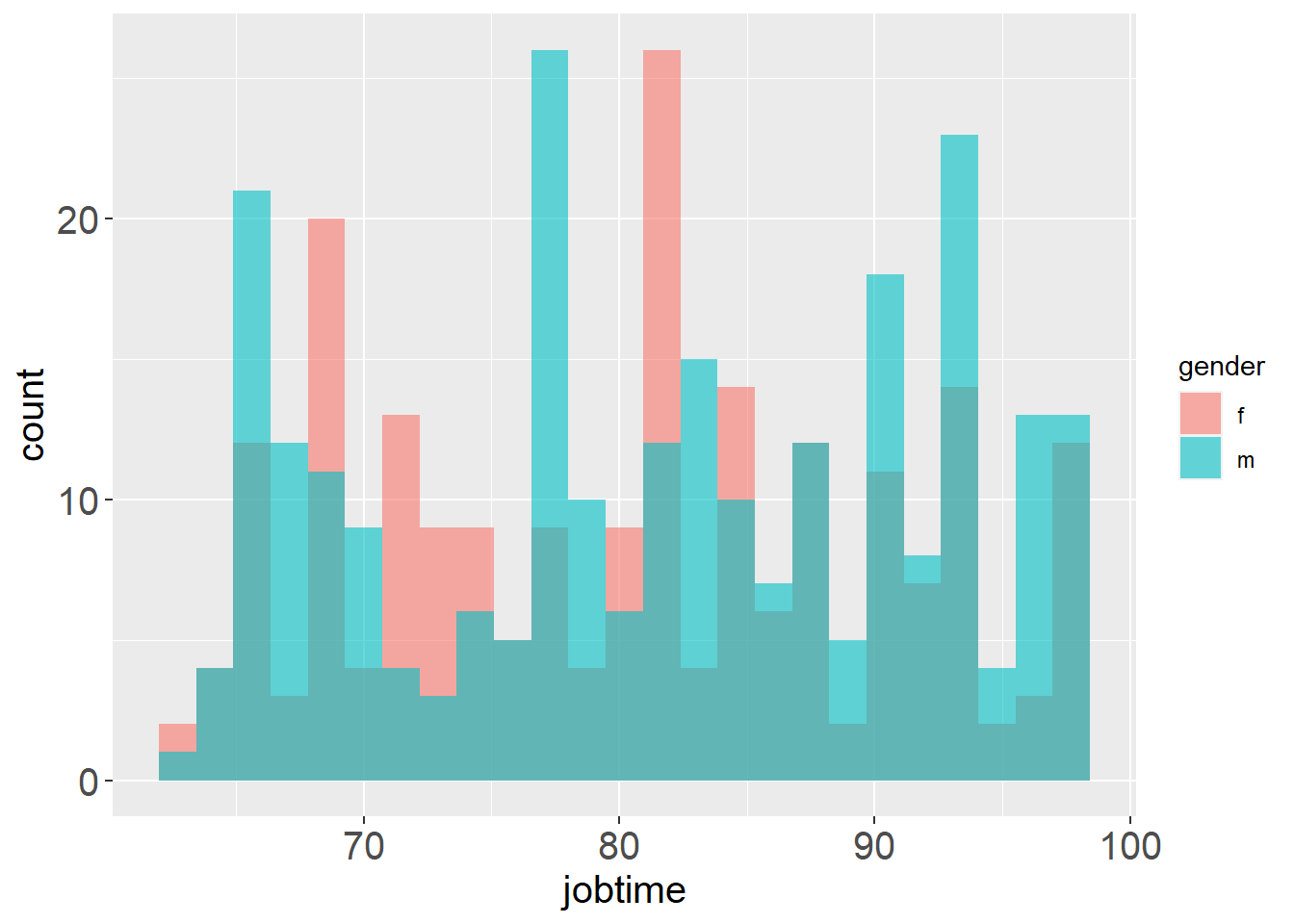

从上图可以看出女性的工作市场在85一周之前是相对比男性多，但是在每周85之后是明显的少于男性工作时长。这也许是因为男性从事的工作的时间长度明显大于女性。

不同起始薪资与收入的关系

ggplot(data = data2,aes(x = salbegin))+geom_histogram(binwidth = 500,color = "blue")+geom_freqpoly(mapping = aes(x=salary),binwidth = 500,color = "red")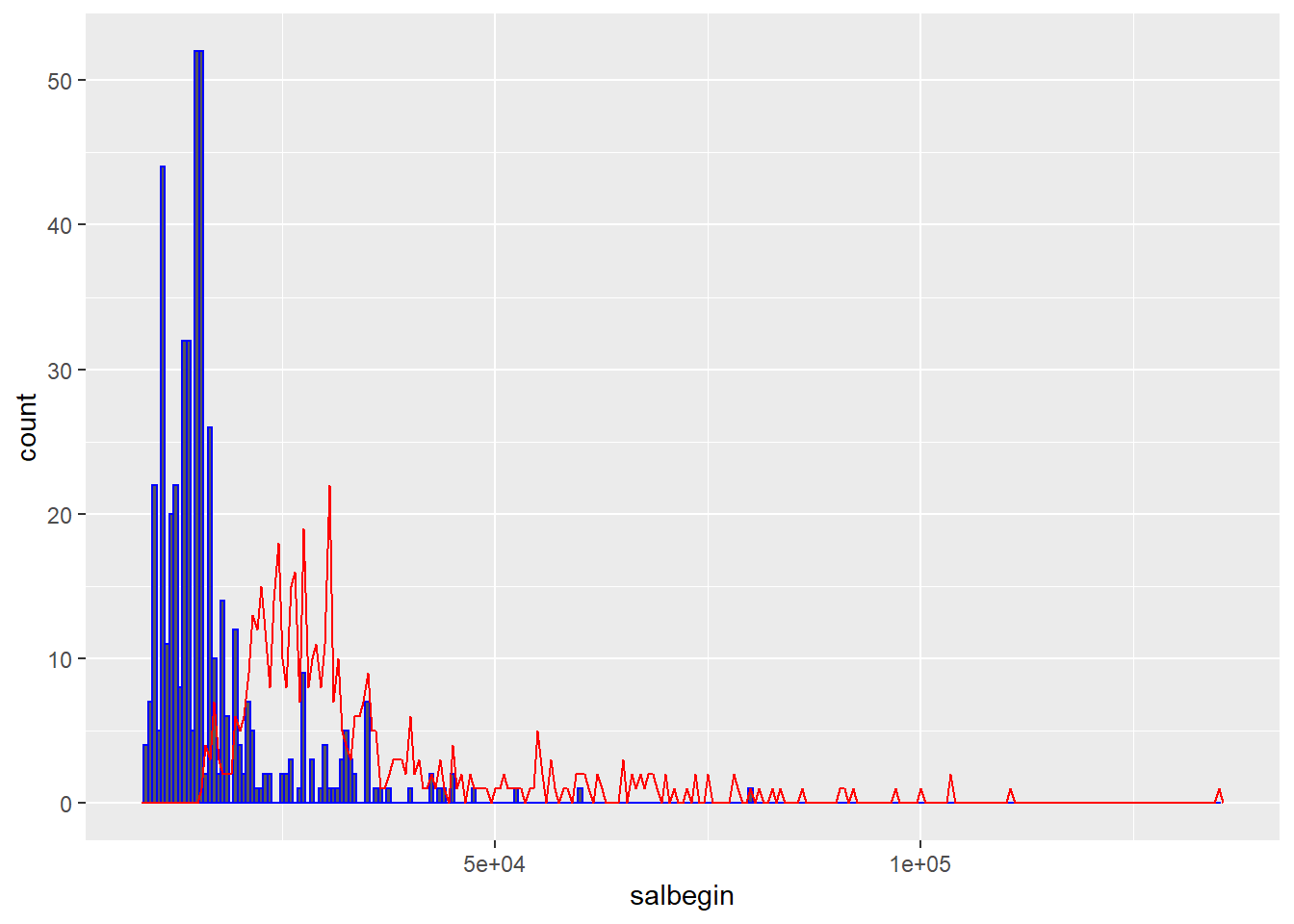

上图纵轴是计数，横轴是起始薪资和当前薪资。直方图代表起始薪资，折线图代表现在的薪资。从上图看出，基本上当前的薪资都会比起始薪资高，并且数据都是在峰值左边较为聚集，在峰值右边明显的分散。

薪资数据建模分析。

通过之前的描述分析我们大致对数据有了初步的认识和判断，接着对数据进行建模分析。在这个问题中，薪资为因变量，自变量中含有因子类型的数据。首先使用传统的线性回归建立模型

options(scipen = 200)
data3<-read.csv("Employee.csv",header = T)
data3$gender<-as.factor(data3$gender)#将性别转化为因子型
data3$minority<-as.factor(data3$minority)#将少数民族转化为因子型
model1<-lm(salary~educ+jobcat+salbegin+jobtime+prevexp+minority+gender,data=data3)
summary(model1)

## 
## Call:
## lm(formula = salary ~ educ + jobcat + salbegin + jobtime + prevexp + 
##     minority + gender, data = data3)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -22901  -3159   -744   2621  46291 
## 
## Coefficients:
##                 Estimate   Std. Error t value             Pr(>|t|)    
## (Intercept) -13610.92441   3007.16431  -4.526       0.000007634730 ***
## educ           470.05170    153.56653   3.061              0.00233 ** 
## jobcat        5760.34182    621.45145   9.269 < 0.0000000000000002 ***
## salbegin         1.31956      0.07011  18.821 < 0.0000000000000002 ***
## jobtime        149.98267     31.32723   4.788       0.000002270406 ***
## prevexp        -20.94984      3.32098  -6.308       0.000000000656 ***
## minority1     -987.39645    784.18450  -1.259              0.20861    
## genderm       2139.92620    735.59361   2.909              0.00380 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6805 on 466 degrees of freedom
## Multiple R-squared:  0.8435, Adjusted R-squared:  0.8412 
## F-statistic: 358.9 on 7 and 466 DF,  p-value: < 0.00000000000000022

将薪资作为自变量，受教育年限，职位等级，起始薪资，工作经验，工作时长，性别，作为因变量，建模线性回归模型。最终的模型为\(y=-13610.92+470.05*educ+5760*jobcat+1.31*salbegin+149.98*jobtime-20.94*prevexp-987.39*minority+2139.92*gender\)。但是发现模型的minority变量没有通过检验，不显著，因此考虑剔除该变量。

模型的检验

par(mfrow=c(2,2))
plot(model1,which = c(1:4))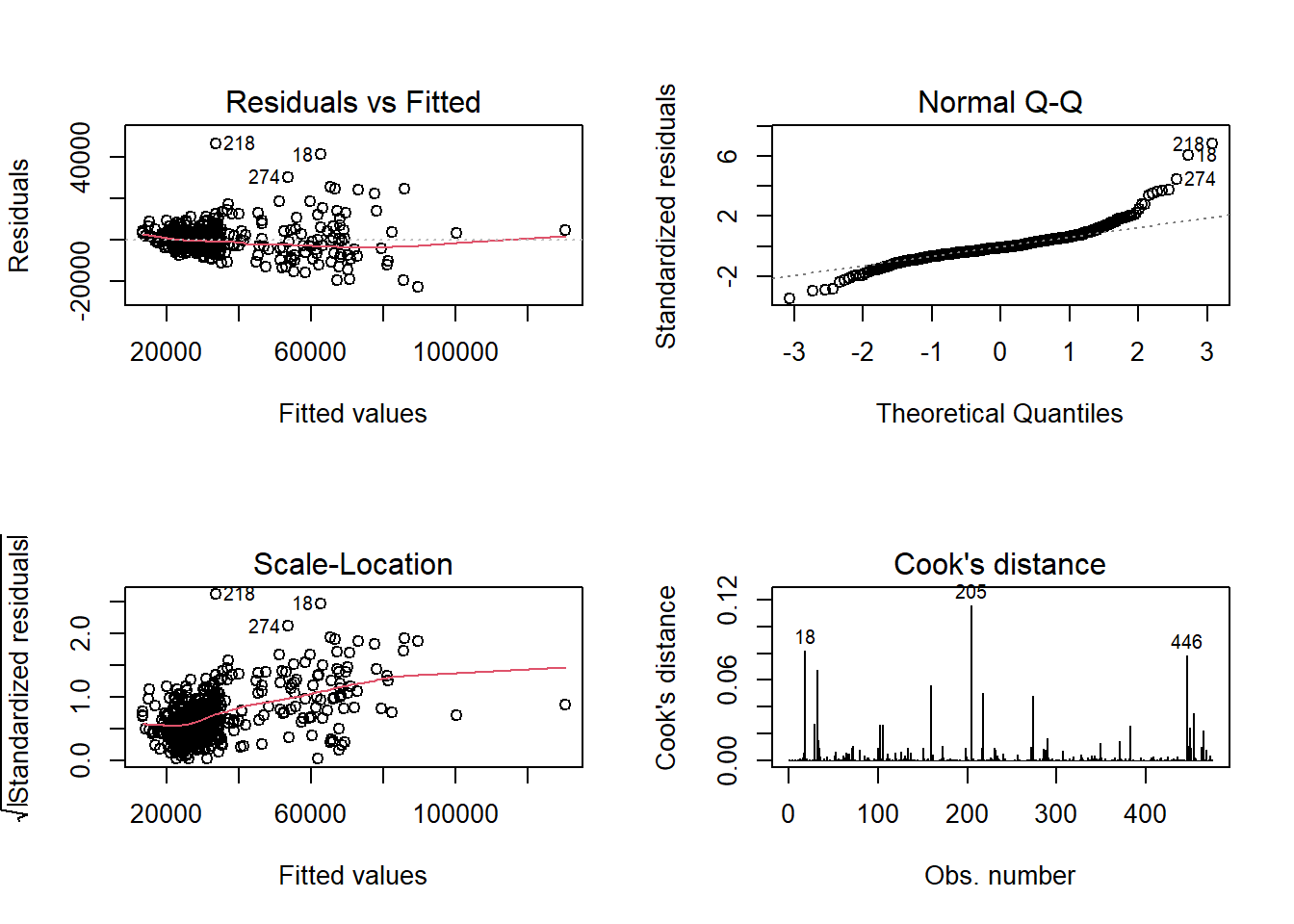

library(equatiomatic)

加权最小二乘建模

通过上面四张图看出该模型有一定的异方差性，需要进行加权建模。这里我们将权重设置为，salbegin,jobcat和jobtime三个变量的平方分之一，接着对模型进行分析。

model2<-lm(salary~educ+jobcat+salbegin+jobtime+prevexp+gender,data=data3)
resd<-model2$residuals
resd<-abs(resd)
summary(model2)

## 
## Call:
## lm(formula = salary ~ educ + jobcat + salbegin + jobtime + prevexp + 
##     gender, data = data3)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -22924  -3272   -670   2606  46565 
## 
## Coefficients:
##                Estimate  Std. Error t value             Pr(>|t|)    
## (Intercept) -13822.1833   3004.3615  -4.601       0.000005431508 ***
## educ           471.8788    153.6559   3.071              0.00226 ** 
## jobcat        5802.3314    620.9449   9.344 < 0.0000000000000002 ***
## salbegin         1.3284      0.0698  19.030 < 0.0000000000000002 ***
## jobtime        148.5239     31.3254   4.741       0.000002824209 ***
## prevexp        -21.4462      3.2996  -6.500       0.000000000207 ***
## genderm       2005.0468    728.2081   2.753              0.00613 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6809 on 467 degrees of freedom
## Multiple R-squared:  0.843,  Adjusted R-squared:  0.841 
## F-statistic: 417.9 on 6 and 467 DF,  p-value: < 0.00000000000000022

model3<-lm(salary~educ+jobcat+salbegin+jobtime+prevexp+gender,data=data3,weights = salbegin^{-2}+jobcat^{-2}+jobtime^{-2})
summary(model3)

## 
## Call:
## lm(formula = salary ~ educ + jobcat + salbegin + jobtime + prevexp + 
##     gender, data = data3, weights = salbegin^{
##     -2
## } + jobcat^{
##     -2
## } + jobtime^{
##     -2
## })
## 
## Weighted Residuals:
##    Min     1Q Median     3Q    Max 
## -14296  -2708   -642   2020  46853 
## 
## Coefficients:
##                 Estimate   Std. Error t value             Pr(>|t|)    
## (Intercept) -12406.52132   2399.42065  -5.171    0.000000346681527 ***
## educ           446.91621    121.49125   3.679             0.000262 ***
## jobcat        5055.52805    886.57803   5.702    0.000000020991222 ***
## salbegin         1.45811      0.08887  16.407 < 0.0000000000000002 ***
## jobtime        121.53179     23.96567   5.071    0.000000571490307 ***
## prevexp        -18.95859      2.54655  -7.445    0.000000000000472 ***
## genderm       1511.88296    553.91437   2.729             0.006584 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4656 on 467 degrees of freedom
## Multiple R-squared:  0.717,  Adjusted R-squared:  0.7134 
## F-statistic: 197.2 on 6 and 467 DF,  p-value: < 0.00000000000000022

#计算model3残差
e<-resid(model3)
abse<-abs(e)
y.fit<-predict(model3)
biaozhunhua<-scale(e)
sqrtcancha<-sqrt(biaozhunhua)

## Warning in sqrt(biaozhunhua): 产生了NaNs

plot(sqrtcancha~y.fit)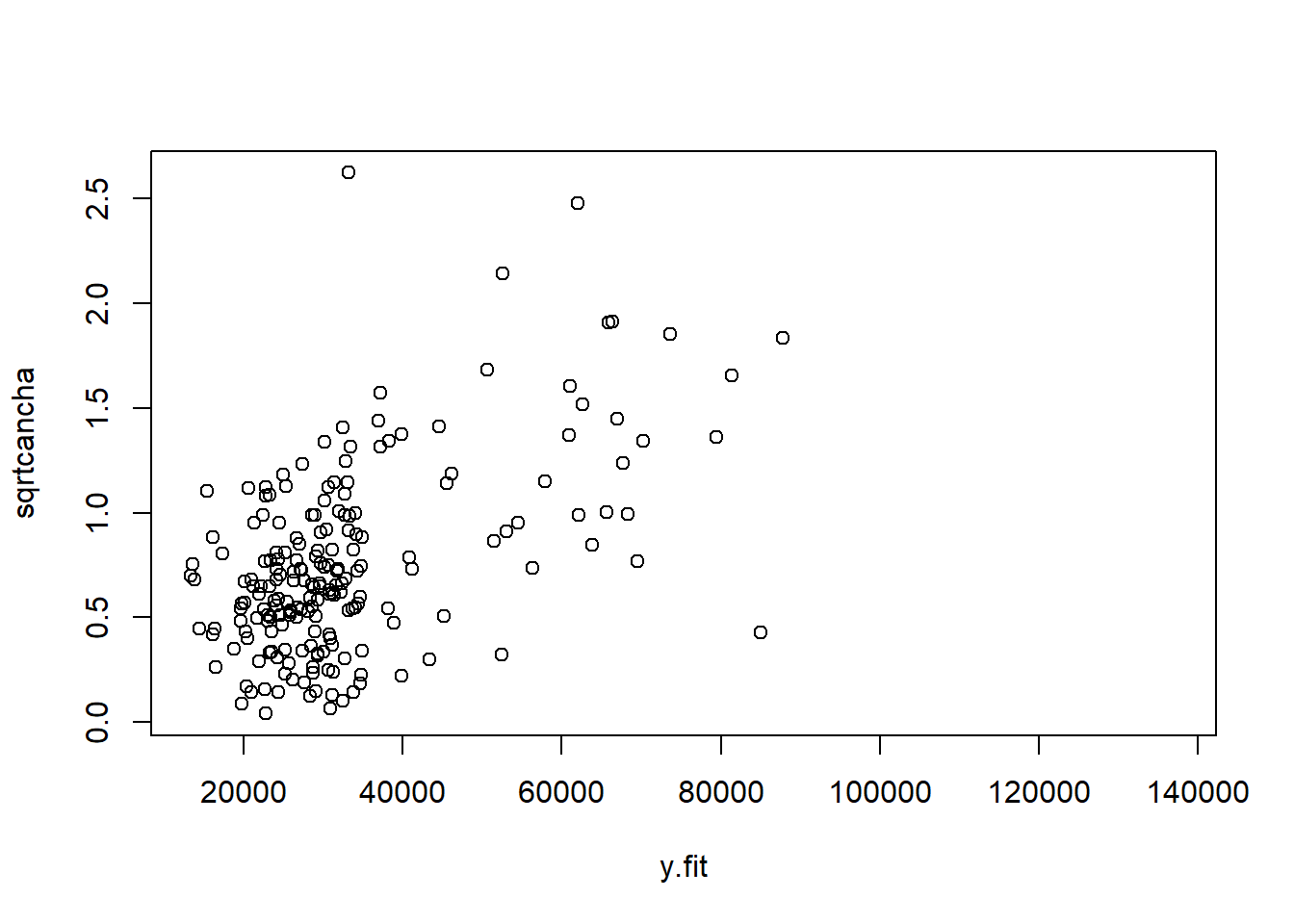

模型的表达式如下 \[ \operatorname{salary} = \alpha + \beta_{1}(\operatorname{educ}) + \beta_{2}(\operatorname{jobcat}) + \beta_{3}(\operatorname{salbegin}) + \beta_{4}(\operatorname{jobtime}) + \beta_{5}(\operatorname{prevexp}) + \beta_{6}(\operatorname{gender}_{\operatorname{m}}) + \epsilon \]

进行加权和未进行加权比较

未进行加权建模图

(

par(mfrow=c(2,2))
plot(model2,which = c(1:4),caption = "model2未加权")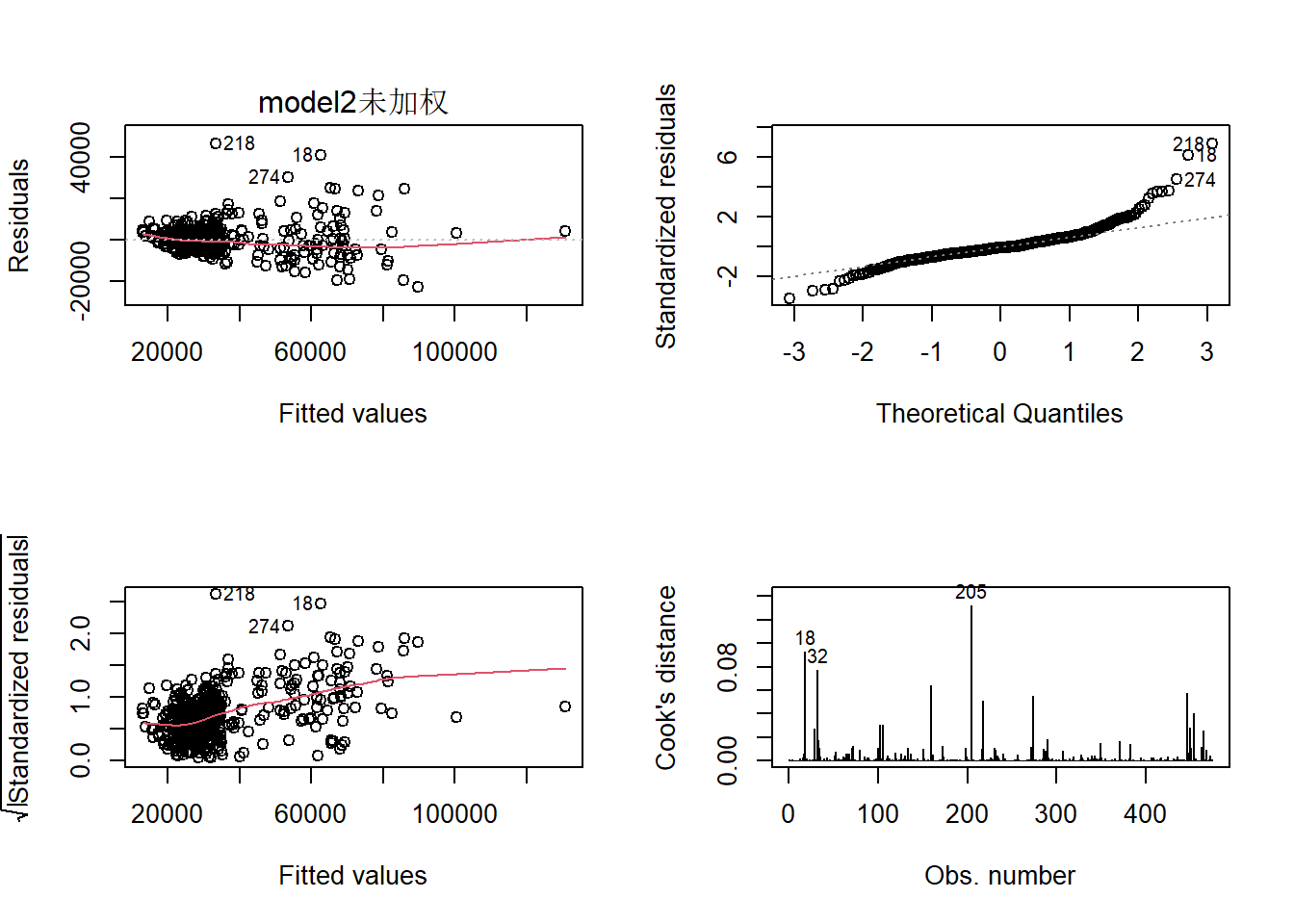

)

进行加权建模图

(

par(mfrow=c(2,2))
plot(model3,which = c(1:4),caption = "model3加权建模")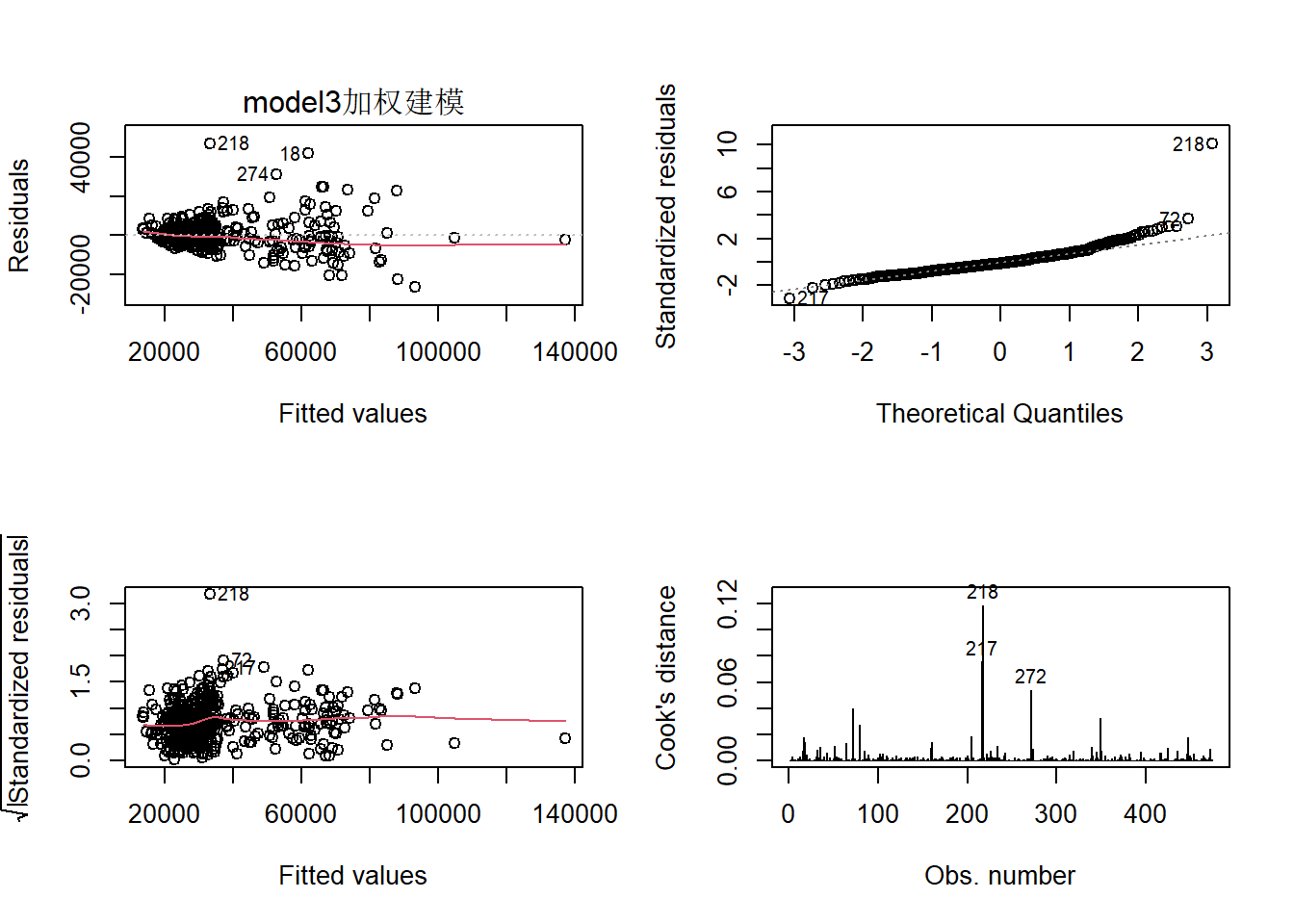

)

通过上图看出,通过加权可以解决模型的异方差性。

检验多重共线性

library(car)

## 载入需要的程辑包：carData

## 
## 载入程辑包：'car'

## The following object is masked from 'package:dplyr':
## 
##     recode

## The following object is masked from 'package:purrr':
## 
##     some

round(vif(model3),2)

##     educ   jobcat salbegin  jobtime  prevexp   gender 
##     1.53     1.54     2.32     1.02     1.11     1.33

上述变量都小于10并且接近1，说明没有多重共线性问题。

变量选择

在这里其实我感觉是不需要再进行变量选择的，因为模型已经解决了异方差性和多重共线性问题。但是课件上面讲了这些，还是做一下。

modelstep<-step(model3,direction = "both")#使用逐步回归法

## Start:  AIC=8013.64
## salary ~ educ + jobcat + salbegin + jobtime + prevexp + gender
## 
##            Df  Sum of Sq         RSS    AIC
## <none>                   10123086798 8013.6
## - gender    1  161490564 10284577362 8019.1
## - educ      1  293331236 10416418034 8025.2
## - jobtime   1  557438393 10680525190 8037.0
## - jobcat    1  704847552 10827934349 8043.5
## - prevexp   1 1201449131 11324535929 8064.8
## - salbegin  1 5835365806 15958452603 8227.4

summary(modelstep)

## 
## Call:
## lm(formula = salary ~ educ + jobcat + salbegin + jobtime + prevexp + 
##     gender, data = data3, weights = salbegin^{
##     -2
## } + jobcat^{
##     -2
## } + jobtime^{
##     -2
## })
## 
## Weighted Residuals:
##    Min     1Q Median     3Q    Max 
## -14296  -2708   -642   2020  46853 
## 
## Coefficients:
##                 Estimate   Std. Error t value             Pr(>|t|)    
## (Intercept) -12406.52132   2399.42065  -5.171    0.000000346681527 ***
## educ           446.91621    121.49125   3.679             0.000262 ***
## jobcat        5055.52805    886.57803   5.702    0.000000020991222 ***
## salbegin         1.45811      0.08887  16.407 < 0.0000000000000002 ***
## jobtime        121.53179     23.96567   5.071    0.000000571490307 ***
## prevexp        -18.95859      2.54655  -7.445    0.000000000000472 ***
## genderm       1511.88296    553.91437   2.729             0.006584 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4656 on 467 degrees of freedom
## Multiple R-squared:  0.717,  Adjusted R-squared:  0.7134 
## F-statistic: 197.2 on 6 and 467 DF,  p-value: < 0.00000000000000022

上面是使用逐步回归法模型。其实可以使用这个来消除多重共线性等问题。

总结

通过各种方法，解决了异方差性和多重共线性，本文最终建立的模型如下： \[ salary=-12406.52+446.91*educ+5055.52*jobcat+1.45*salbegin+121.53*jobtime-18.95*prevexp+1511.88*gender \]